题目内容
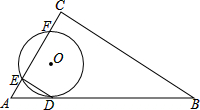 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π.(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
考点:切线的性质,弧长的计算
专题:几何综合题
分析:(1)要证明DE∥BC,可证明∠EDA=∠B,由弧DE的长度为4π,可以求得∠DOE的度数,再根据切线的性质可求得∠EDA的度数,即可证明结论.
(2)根据90°的圆周角对的弦是直径,可以求得EF,的长度,借用勾股定理求得AE与CF的长度,即可得到答案.
(2)根据90°的圆周角对的弦是直径,可以求得EF,的长度,借用勾股定理求得AE与CF的长度,即可得到答案.
解答:解:(1)证明:连接OD、OE,

∵AD是⊙O的切线,
∴OD⊥AB,∴∠ODA=90°,
又∵弧DE的长度为4π,
∴4π=
,
∴n=60,
∴△ODE是等边三角形,
∴∠ODE=60°,∴∠EDA=30°,
∴∠B=∠EDA,
∴DE∥BC.
(2)连接FD,

∵DE∥BC,
∴∠DEF=∠C=90°,
∴FD是⊙0的直径,
由(1)得:∠EFD=
∠EOD=30°,FD=24,
∴EF=12
,
又∵∠EDA=30°,DE=12,
∴AE=4
,
又∵AF=CE,∴AE=CF,
∴CA=AE+EF+CF=20
,
又∵tan∠ABC=tan30°=
=
,
∴BC=60.

∵AD是⊙O的切线,
∴OD⊥AB,∴∠ODA=90°,
又∵弧DE的长度为4π,
∴4π=
| nπ×12 |
| 180 |
∴n=60,
∴△ODE是等边三角形,
∴∠ODE=60°,∴∠EDA=30°,
∴∠B=∠EDA,
∴DE∥BC.
(2)连接FD,

∵DE∥BC,
∴∠DEF=∠C=90°,
∴FD是⊙0的直径,
由(1)得:∠EFD=
| 1 |
| 2 |
∴EF=12
| 3 |
又∵∠EDA=30°,DE=12,
∴AE=4
| 3 |
又∵AF=CE,∴AE=CF,
∴CA=AE+EF+CF=20
| 3 |
又∵tan∠ABC=tan30°=
| AC |
| BC |
| ||
| 3 |
∴BC=60.
点评:本题考查了勾股定理以及圆的性质的综合应用,解答本题的关键在于90°的圆周角对的弦是直径这一性质的灵活运用.

练习册系列答案
相关题目
 如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.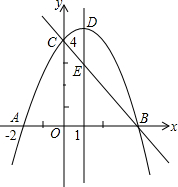 如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.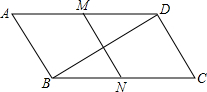 如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.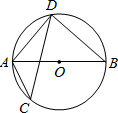 如图,AB为⊙O直径,CD为⊙O的弦,∠ACD=25°,∠BAD的度数为
如图,AB为⊙O直径,CD为⊙O的弦,∠ACD=25°,∠BAD的度数为