题目内容
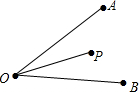已知如图∠AOB=45°，OP=1，在OA、OB上任取两点M、N，得△PMN，求△PMN周长的最小值是考点：轴对称-最短路线问题
专题：
分析：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．
解答：
解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．
∵PC关于OA对称，
∴∠COP=2∠AOP，OC=OP，
同理，∠DOP=2∠BOP，OP=OD，
∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．
∴△COD是等腰直角三角形，
∴CD=
OC=
．
故答案为：
．
解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，
∴∠COP=2∠AOP，OC=OP，
同理，∠DOP=2∠BOP，OP=OD，
∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．
∴△COD是等腰直角三角形，
∴CD=
| 2 |
| 2 |
故答案为：
| 2 |
点评：本题考查了对称的性质，等腰直角三角形的判定和性质以及勾股定理的运用，解题的关键是正确作出图形，理解△PMN周长最小的条件是解题的关键．
练习册系列答案
相关题目
在四边形ABDC中，若∠A=∠C=90°，2∠A=3∠D，则∠B=在平面内，如果一个角的两边与另一个角的两边平行，则这两个角数量关系是（ ）
| A、相等 | B、互余或互补 |
| C、相等或互余 | D、相等或互补 |