题目内容
20．
如图，在△ABC中，AB=AC，AD平分∠CAB，N点是AB上的一定点，M是AD上一动点，要使MB+MN最小，请找出点E的位置．
分析 作点N关于AD的对称点N′，连接BN′交AD于点M，由两点之间线段最短可知M点即为所求点．
解答 
解：①作点N关于AD的对称点N′，连接BN′交AD于点M，
②由对称的性质可知MN=MN′，故MN+BM=BN′，
③由两点之间线段最短可知，MB+MN最小．
点评 本题考查的是最短线路问题，根据两点之间线段最短的知识作出N的对称点是解答此题的关键．
练习册系列答案
相关题目
8．若有理数a，b，c在数轴上的对应点如图所示．
化简：|a+b|+|c+b|+|c-a|=（ ）
化简：|a+b|+|c+b|+|c-a|=（ ）
| A． | 2a-2c | B． | 2a+2b | C． | 2b+2c | D． | 0 |
已知有理数a、b、c在数轴上的位置如图所示，试化简|a|+|b|-|c|+|a-b|-|b+c|．
12．
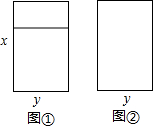如图①，图②是宏达门窗厂制作的两种同大小的长方形铝合金窗框，已知窗框的长都是x米，窗框的宽都是y米．若王阿婆家装修需要图①窗框2个，图②窗框5个，则制作这些窗框需要铝合金多少米（接缝忽略不计）？
如图①，图②是宏达门窗厂制作的两种同大小的长方形铝合金窗框，已知窗框的长都是x米，窗框的宽都是y米．若王阿婆家装修需要图①窗框2个，图②窗框5个，则制作这些窗框需要铝合金多少米（接缝忽略不计）？
9．已知两点A（-5，y1），B（3，y2）均在抛物线y=ax2+bx+c（a≠0）上，点C（x0，y0）是该抛物线的顶点．若y1＜y2≤y0，则x0的取值范围是（ ）
| A． | x0＞-1 | B． | x0＜-1 | C． | -5＜x0＜-1 | D． | -1＜x0＜3 |