题目内容
已知2x2+10x+1=0,那么多项式(x+1)(x+2)(x+3)(x+4)的值为 .
考点:整式的混合运算—化简求值
专题:
分析:先根据式子的特点展开,最后求出x2+5x的值,再代入求出即可.
解答:解:∵2x2+10x+1=0,
∴2x2+10x=-1,
∴x2+5x=-
∴(x+1)(x+2)(x+3)(x+4)
=(x+1)(x+4)(x+2)(x+3)
=(x2+5x+4)(x2+5x+6)
=(x2+5x)2+10(x2+5x)+24
=(-
)2+10×(-
)+24
=19
,
故答案为:19
.
∴2x2+10x=-1,
∴x2+5x=-
| 1 |
| 2 |
∴(x+1)(x+2)(x+3)(x+4)
=(x+1)(x+4)(x+2)(x+3)
=(x2+5x+4)(x2+5x+6)
=(x2+5x)2+10(x2+5x)+24
=(-
| 1 |
| 2 |
| 1 |
| 2 |
=19
| 1 |
| 4 |
故答案为:19
| 1 |
| 4 |
点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算和化简能力,题目比较好,难度适中.

练习册系列答案
相关题目
下列各数中,最小的数是( )
| A、-2 | B、-1 | C、0 | D、2 |
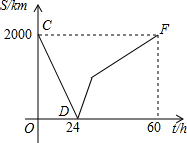 如图所示,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,设慢车行驶时间为t小时,两车之间的距离为s千米,图中折线表示s与t之间的函数关系,当两车距离不超过200千米,两车可用车载电话通话,则两车可用车载电话通话的时间是
如图所示,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,设慢车行驶时间为t小时,两车之间的距离为s千米,图中折线表示s与t之间的函数关系,当两车距离不超过200千米,两车可用车载电话通话,则两车可用车载电话通话的时间是 如图,将直线y=x向右平移2个单位后与双曲线y=
如图,将直线y=x向右平移2个单位后与双曲线y=