题目内容
7. 如图,菱形ABD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
如图,菱形ABD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )| A. | 1:$\sqrt{3}$ | B. | 1:$\sqrt{2}$ | C. | 1:3 | D. | 1:2 |
分析 根据菱形的性质得出∠ABD=∠CBD,AC⊥BD,OD=OB,OA=OC,AB=BC=CD=AD=2cm,在Rt△AEB中,解直角三角形求出OA:OB,即可求出答案.
解答 解:
∵菱形ABD的周长为8cm,高AE长为$\sqrt{3}$cm,
∴∠ABD=∠CBD,AC⊥BD,OD=OB,OA=OC,AB=BC=CD=AD=2cm,∠AEB=90°,
∴sin∠ABE=$\frac{AE}{AB}$=$\frac{\sqrt{3}}{2}$,
即∠ABC=60°,
∴∠ABD=30°,
∴$\frac{AC}{BD}$=$\frac{2OA}{2OB}$=$\frac{OA}{OB}$=$\frac{1}{\sqrt{3}}$=1:$\sqrt{3}$,
故选A.
点评 本题考查了菱形的性质,能熟记菱形的性质是解此题的关键,注意:菱形的四条边都相等,菱形的对角线互相垂直且平分,并且每一条对角线平分一组对角.

练习册系列答案
相关题目
18.数轴上表示6的点,移动2个单位后,这个点表示的数是( )
| A. | 4或-4 | B. | 8 | C. | -4 | D. | 4或8 |
15.在平面直角坐标系中,点P(3,-1)关于x轴对称的点的坐标是( )
| A. | (-3,-1) | B. | (-3,1) | C. | (-1,3) | D. | (3,1) |
12.我市某中学九年级学生对市民“创建精神文明城市”知晓率采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解“、“从未听说”五个等级,统计后的数据整理如下表:
(1)表中m的值为0.3;
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数;
(3)根据上述统计结果,请你对政府相关部门提出一句话建议.
| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 | 从未听说 |
| 频数 | 40 | 60 | 48 | 36 | 16 |
| 频率 | 0.2 | m | 0.24 | 0.18 | 0.08 |
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数;
(3)根据上述统计结果,请你对政府相关部门提出一句话建议.
 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).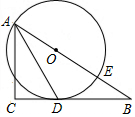 如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,求BD的长.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,求BD的长.