题目内容
18.(1)计算:(-1)2+cos60°-$\root{3}{8}$(2)计算:($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$.
分析 (1)原式第一项利用乘方的意义化简,第二项利用特殊角的三角函数值计算,最后一项利用立方根定义计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=1+$\frac{1}{2}$-2=-$\frac{1}{2}$;
(2)原式=[$\frac{a}{(a+b)(a-b)}$-$\frac{a-b}{(a+b)(a-b)}$]•$\frac{b-a}{b}$=$\frac{b}{(a+b)(a-b)}$•$\frac{-(a-b)}{b}$=-$\frac{1}{a+b}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列图形中,由∠1=∠2能得到AB∥CD的是( )
| A. |  | B. |  | ||
| C. |  | D. | 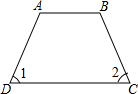 |
6.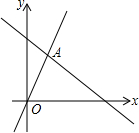 如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(3,m)则不等式kx≥-$\frac{1}{2}$x+4的解集为( )
如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(3,m)则不等式kx≥-$\frac{1}{2}$x+4的解集为( )
 如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(3,m)则不等式kx≥-$\frac{1}{2}$x+4的解集为( )
如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(3,m)则不等式kx≥-$\frac{1}{2}$x+4的解集为( )| A. | x≥3 | B. | x≤3 | C. | x≤2 | D. | x≥2 |
8.小李随机调查了7辆不同品牌汽车的百公里油耗如表:
这7辆不同品牌汽车百公里油耗的中位数是9.3升.
| 品牌 | A | B | C | D | E | F | G |
| 百公里油耗(升) | 8.1 | 9.3 | 12.5 | 9 | 11 | 13 | 7.6 |
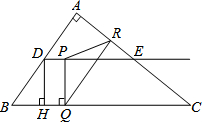 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.如果在点P运动的过程中,使△PQR成为等腰三角形,则x的值是$\frac{18}{5}$、6、$\frac{15}{2}$.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.如果在点P运动的过程中,使△PQR成为等腰三角形,则x的值是$\frac{18}{5}$、6、$\frac{15}{2}$.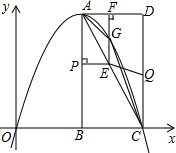 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动,运动速度为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1,0),C(3,0),D(3,4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动,运动速度为每秒1个单位.运动时间为t秒.过点P作PE⊥AB交AC于点E.


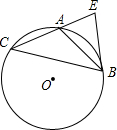 如图,△ABC内接于⊙O,过点B作⊙O的切线,交CA的延长线于点E,∠EBC=2∠C.
如图,△ABC内接于⊙O,过点B作⊙O的切线,交CA的延长线于点E,∠EBC=2∠C.