题目内容
10.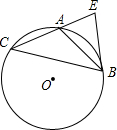 如图,△ABC内接于⊙O,过点B作⊙O的切线,交CA的延长线于点E,∠EBC=2∠C.
如图,△ABC内接于⊙O,过点B作⊙O的切线,交CA的延长线于点E,∠EBC=2∠C.(1)求证:AB=AC;
(2)当$\frac{AB}{BC}$=$\frac{\sqrt{5}}{4}$,求tan∠ABE的值.
分析 (1)由BE为圆O的切线,BA为圆的弦,即∠EAB为圆弦切角,根据弦切角等于所夹弧所对的圆周角,可得出∠EBA=∠C,根据已知的∠EBC=2∠C,得到∠ABC=∠C,根据等角对等边可得出AB=AC,得证;
(2)连接OA,由AB=AC,根据等弦对等劣弧得到A为弧BC的中点,根据垂径定理的逆定理得到OA垂直于BC,D为BC的中点,再由∠C=∠ABC=∠ABE,在Rt△ABD中,tan∠ABC=$\frac{AD}{BD}$=$\frac{1}{2}$,得到tan∠ABE=tan∠ABC=$\frac{1}{2}$.
解答 解:(1)∵BE为圆O的切线,BA为圆的弦,
∴∠EBA为弦切角,
∴∠EBA=∠C,又∠EBC=2∠C,
∴∠EBC=2∠EBA,
∴∠ABC=∠C,
∴AB=AC;
(2)连接OA,由(1)证得AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,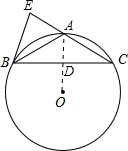
∴OA⊥BC,
∴D为BC的中点,即BD=CD,
∵$\frac{AB}{BC}$=$\frac{\sqrt{5}}{4}$,
设AB=$\sqrt{5}$k,BC=4k,
∴BD=$\frac{1}{2}$BC=2k,
∴AD=$\sqrt{{AB}^{2}{-BD}^{2}}$=k,
∵∠C=∠ABC=∠ABE,
∴tan∠ABE=tan∠ABC
在Rt△ABD中,tan∠ABC=$\frac{AD}{BD}$=$\frac{1}{2}$,
∴tan∠ABE=tan∠ABC=$\frac{1}{2}$.
点评 考查了切线的性质,等腰三角形的判定与性质,弦、圆心角及弧之间的关系,勾股定理,垂径定理,圆周角定理,相似三角形的判定与性质,以及锐角三角函数定义,熟练掌握性质及定理是解本题的关键.

练习册系列答案
相关题目
2.计算(-3)-(-5)的结果等于( )
| A. | -2 | B. | 2 | C. | -8 | D. | 15 |
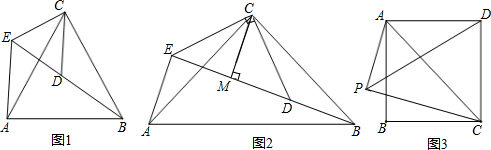
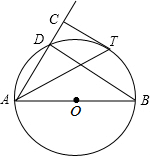 如图,AB是⊙O的直径,D为⊙O上一点,过$\widehat{BD}$上一点T作⊙O的切线TC,且TC⊥AD于点C.
如图,AB是⊙O的直径,D为⊙O上一点,过$\widehat{BD}$上一点T作⊙O的切线TC,且TC⊥AD于点C.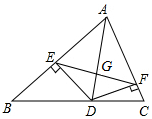 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,EF与AD相交于点G.
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,EF与AD相交于点G.