题目内容
10.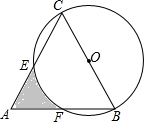 如图,△ABC是等边三角形,以BC为直径作圆O,交AC、AB于E、F两点,若AB=4,则阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,△ABC是等边三角形,以BC为直径作圆O,交AC、AB于E、F两点,若AB=4,则阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
分析 先连接OE,OF,再根据△ABC是等边三角形得到△COE和△BOF都是等边三角形,最后根据S阴影=S△ABC-S扇形EOF-2S△COE进行计算即可.
解答  解:如图,连接OE,OF,
解:如图,连接OE,OF,
∵△ABC是等边三角形,AB=4,
∴OC=OE=OB=OF=2,∠FBO=∠ECO=60°,
∴△COE和△BOF都是等边三角形,
∴∠EOF=180°-120°=60°,
∴S阴影=S△ABC-S扇形EOF-2S△COE=4$\sqrt{3}$-$\frac{60×π×{2}^{2}}{360}$-2×$\sqrt{3}$=2$\sqrt{3}$-$\frac{2}{3}$π.
故答案为:2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题主要考查了扇形面积的计算以及等边三角形的判定与性质的运用,解题时注意:求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.

练习册系列答案
相关题目
1.已知x<y,则下列式子不正确的是( )
| A. | 4x<4y | B. | -4x<-4y | C. | x+4<y+4 | D. | x-4<y-4 |
5.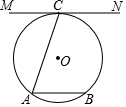 如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )
如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )
 如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )
如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{4}$ | C. | 2 | D. | $\frac{\sqrt{5}}{2}$ |
15. 如图,转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点M落在直线y=x的下方的概率为( )
如图,转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点M落在直线y=x的下方的概率为( )
 如图,转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点M落在直线y=x的下方的概率为( )
如图,转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点M落在直线y=x的下方的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |

 如图,经过原点的抛物线y=-x2+2mx(m>1)交x轴正半轴于点A,过点P(1,m)作直线PD⊥x轴于点D,交抛物线于点B,记点B关于抛物线对称轴的对称点为C,连结CB,CP.
如图,经过原点的抛物线y=-x2+2mx(m>1)交x轴正半轴于点A,过点P(1,m)作直线PD⊥x轴于点D,交抛物线于点B,记点B关于抛物线对称轴的对称点为C,连结CB,CP.