题目内容
5.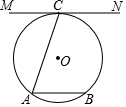 如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )
如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC=$\sqrt{5}$,则⊙O的半径为( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{4}$ | C. | 2 | D. | $\frac{\sqrt{5}}{2}$ |
分析 延长CO交AB于D,根据切线的性质得到OC⊥MN,根据平行线的性质、勾股定理求出CD,设⊙O的半径为r,根据勾股定理列出方程,解方程求出r即可.
解答  解:连接CO并延长交AB于D,连接OA,
解:连接CO并延长交AB于D,连接OA,
∵MN是⊙O的切线,
∴MN⊥CD,
∵MN∥AB,
∴CD⊥AB,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×2=1,
在Rt△ACD中,AC=$\sqrt{5}$,
由勾股定理得:CD=$\sqrt{(\sqrt{5})^{2}-{1}^{2}}$=2,
设⊙O的半径为r,则OD=2-r,OA=r,
在Rt△AOD中,r2=12+(2-r)2,
r=$\frac{5}{4}$,
则⊙O的半径为$\frac{5}{4}$;
故选B.
点评 本题考查的是切线的性质、勾股定理的应用、平行线的性质,掌握圆的切线垂直于经过切点的半径是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16.已知△ABC的三边分别是6,8,10,则△ABC的面积是( )
| A. | 24 | B. | 30 | C. | 40 | D. | 48 |
13.下列由左边到右边的变形,是因式分解的是( )
| A. | am+bm-1=m(a+b)-1 | B. | (x+2)(x-5)=x2-3x-10 | C. | x2+5x+4=x(x+5+$\frac{4}{x}$) | D. | x2-4x=x(x-4) |
17.测得某人一根头发的直径约为0.000 071 5米,该数用科学记数法可表示为( )
| A. | 0.715×104 | B. | 0.715×10-4 | C. | 7.15×105 | D. | 7.15×10-5 |
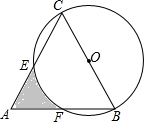 如图,△ABC是等边三角形,以BC为直径作圆O,交AC、AB于E、F两点,若AB=4,则阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,△ABC是等边三角形,以BC为直径作圆O,交AC、AB于E、F两点,若AB=4,则阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.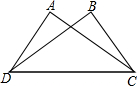 如图,AC=BD,AD=BC,∠DBC=90°,探究AD与AC的位置关系并说明理由?
如图,AC=BD,AD=BC,∠DBC=90°,探究AD与AC的位置关系并说明理由?