题目内容
15. 如图,转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点M落在直线y=x的下方的概率为( )
如图,转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点M落在直线y=x的下方的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
分析 用列表法,把点M的坐标的16种情况都表示出来,可知中落在直线y=x的有(1,1),(2,2),(3,3),(4,4),共4种,所以M点落在落在直线y=x的概率是$\frac{4}{16}$=$\frac{1}{4}$.
解答 解:设M的坐标(x,y),
列表得:
| x y | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
则点(x,y)落在直线y=x上的有(1,1),(2,2),(3,3)(4,4)四种情况,
∴点(x,y)落在直线y=x的概率为$\frac{4}{16}$=$\frac{1}{4}$.
故选A.
点评 本题考查概率的求法与运用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
6.已知三角形三边长为a,b,c,如果$\sqrt{a-6}$+|b-8|+(c-10)2=0,则△ABC是( )
| A. | 以a为斜边的直角三角形 | B. | 以b为斜边的直角三角形 | ||
| C. | 以c为斜边的直角三角形 | D. | 不是直角三角形 |
3. 如图,一把直尺沿直线断开并错位,点E,D,B,F在同一条直线上,若∠ADE=140°,则∠DBC的度数为( )
如图,一把直尺沿直线断开并错位,点E,D,B,F在同一条直线上,若∠ADE=140°,则∠DBC的度数为( )
 如图,一把直尺沿直线断开并错位,点E,D,B,F在同一条直线上,若∠ADE=140°,则∠DBC的度数为( )
如图,一把直尺沿直线断开并错位,点E,D,B,F在同一条直线上,若∠ADE=140°,则∠DBC的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
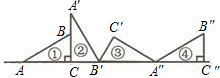 如图所示的直角三角形ABC向右翻滚,下列说法:(1)①到②是旋转;(2)①到③是平移;(3)①到④是平移;(4)②到③是旋转,其中正确的有( )
如图所示的直角三角形ABC向右翻滚,下列说法:(1)①到②是旋转;(2)①到③是平移;(3)①到④是平移;(4)②到③是旋转,其中正确的有( )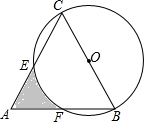 如图,△ABC是等边三角形,以BC为直径作圆O,交AC、AB于E、F两点,若AB=4,则阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,△ABC是等边三角形,以BC为直径作圆O,交AC、AB于E、F两点,若AB=4,则阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π. 某校举办“书香校园”读书活动,经过对八年级(2)班的全体学生的每人每月读书的数量(单位:本)进行统计分析,得到条形统计图如图所示:
某校举办“书香校园”读书活动,经过对八年级(2)班的全体学生的每人每月读书的数量(单位:本)进行统计分析,得到条形统计图如图所示: 如图,将一块三角板的直角顶点放在直尺的一边上.若∠1=38°,则∠2=52°.
如图,将一块三角板的直角顶点放在直尺的一边上.若∠1=38°,则∠2=52°.