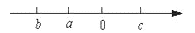题目内容
已知,如图,抛物线与x轴交点坐标为A(1,0),C(-3,0),
(1)若已知顶点坐标D为(-1,4)或B点(0,3),选择适当方式求抛物线的解析式.
(2)若直线DH为抛物线的对称轴,在(1)的基础上,求线段DK的长度,并求△DBC的面积.
(3)将图(2)中的对称轴向左移动,交x轴于点p(m,0)(-3<m<-1),与线段BC、抛物线的交点分别为点K、Q,用含m的代数式表示QK的长度,并求出当m为何值时,△BCQ的面积最大?
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目



 ,
, 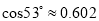 ,
, 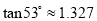 ).
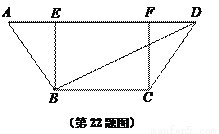
).
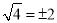 B.
B. 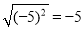 C.
C. 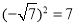 D.
D. 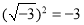
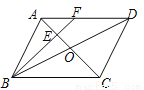
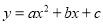 (
(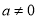 )的图像如图所示,那么下列不等式成立的是( )
)的图像如图所示,那么下列不等式成立的是( )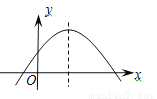
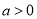 B.
B. 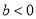 C.
C. 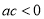 D.
D.