题目内容
9. 如图,在△ABC中,D、E为边AB、AC的中点,己知△ADE的面积为3,那么△ABC的面积是( )
如图,在△ABC中,D、E为边AB、AC的中点,己知△ADE的面积为3,那么△ABC的面积是( )| A. | 6 | B. | 9 | C. | 12 | D. | 15 |
分析 由条件可知DE是△ABC的中位线,根据中位线的性质就可以求出$\frac{DE}{BC}$,再根据相似三角形的性质就可以得出结论.
解答 解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,$\frac{DE}{BC}=\frac{1}{2}$,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2,
∵△ADE的面积为3,
∴$\frac{3}{{S}_{△ABC}}$=$\frac{1}{4}$,
∴S△ABC=12.
故选(C).
点评 本题主要考查了三角形中位线定理的运用,以及相似三角形的判定及性质的运用,解答时运用相似三角形的面积的比等于相似比的平方,是解答本题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
17. 如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )
如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )
 如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )
如图,现有一张矩形纸片(即矩形ABCD),若沿虚线剪去∠C,则∠1+∠2的度数为( )| A. | 180° | B. | 240° | C. | 270° | D. | 330° |
1.在等腰△ABC中,AB=5cm,BC=7cm.则等腰△ABC的周长为( )
| A. | 12cm | B. | 17cm | C. | 19cm | D. | 17cm或19cm |
19.把长宽分别为7和4的长方形经过割补变为一个正方形,这个正方形的边长在( )
| A. | 5与6之间 | B. | 4与5之间 | C. | 3与4之间 | D. | 2与3之间 |
 如图,在△ABC中(AB>AC),AD是BC边上的高,E、F、G分别是BC、AB、AC三边的中点.
如图,在△ABC中(AB>AC),AD是BC边上的高,E、F、G分别是BC、AB、AC三边的中点. 如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD. 如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.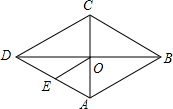 如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为32,则OE的长等于( )
如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为32,则OE的长等于( )