题目内容
2.已知△ABC,∠ABC的平分线BD,∠ACB的平分线CE交于点O,过点O作FO⊥OC,OF交BC于F,连接AO.(1)如图1,求证:∠AOB=∠BFO;
(2)如图2,当∠BAC=90°时,若OD=$\frac{1}{3}$BO,请你探究线段OA和OE的数量关系,并证明你的结论.
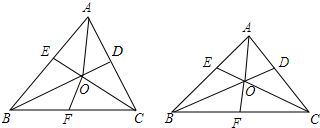
分析 (1)根据三角形内角和定理和三角形外角的性质得出∠AOB=90$°+\frac{1}{2}∠$ACB,∠BFO=90$°+\frac{1}{2}∠$ACB,从而证得∠AOB=∠BFO;
(2)作OG⊥AB于G,OH⊥BC于H,根据角平分线的性质得出OG=OH,进而根据等角的余角相等证得∠OEG=∠OFH,即可证得△OGE≌△OHF,得出OE=OF,由OA是角平分线证得△AGO是等腰直角三角形,根据平行线分线段成比例定理得出$\frac{BG}{AG}$=$\frac{BO}{OD}$=$\frac{3}{1}$,设AG=OG=x,则BG=3x,AB=4x,根据勾股定理求得BO=$\sqrt{A{G}^{2}+O{G}^{2}}$=$\sqrt{10}$x,然后根据△ABO∽△OBF,对应边成比例证得OA=$\frac{2}{5}$$\sqrt{10}$OE.
解答 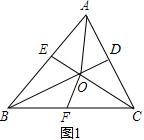 解:(1)如图1,∵∠ABC的平分线BD,∠ACB的平分线CE交于点O,
解:(1)如图1,∵∠ABC的平分线BD,∠ACB的平分线CE交于点O,
∴AO平分∠BAC,
∴∠ABO=$\frac{1}{2}∠$ABC,∠BAO=$\frac{1}{2}∠$BAC,
∵∠ACB=180°-∠ABC-∠BAC,
∴∠AOB=180°-$\frac{1}{2}∠$ABC-$\frac{1}{2}$BAC=180°-$\frac{1}{2}$(∠ABC+∠BAC)=90$°+\frac{1}{2}∠$ACB,
∵FO⊥OC,
∴∠FOC=90°,
∵∠BFO=∠FOC+∠OCF,∠OCF=$\frac{1}{2}∠$ACB,
∴∠BFO=90$°+\frac{1}{2}∠$ACB,
∴∠AOB=∠BFO;
(2)如图2,作OG⊥AB于G,OH⊥BC于H,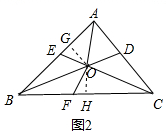
∵BD平分∠ABC,
∴OG=OH,
∵∠BAC=90,FO⊥OC,
∴∠ACE+∠AEC=90°,∠BCE+∠OFC=90°,
∵∠ACE=∠BCE,
∴∠AEC=∠OFC,
在△OGE和△OHF中,
$\left\{\begin{array}{l}{∠OGE=∠OHF=90°}\\{∠GEO=∠HFO}\\{OG=OH}\end{array}\right.$,
∴△OGE≌△OHF(AAS),
∴OE=OF,
∵OG⊥AB,∠BAC=90°,
∴OG∥AC,
∴$\frac{BG}{AG}$=$\frac{BO}{OD}$=$\frac{3}{1}$,
∵OA平分∠BAC,
∴∠GAO=45°,
∴△GAO是等腰直角三角形,
∴AG=OG,
设AG=OG=x,则BG=3x,AB=4x,
∴BO=$\sqrt{A{G}^{2}+O{G}^{2}}$=$\sqrt{10}$x,
由(1)可知:∠AOB=∠BFO,
∵∠ABO=∠OBF,
∴△ABO∽△OBF,
∴$\frac{AO}{OF}$=$\frac{AB}{OB}$=$\frac{4x}{\sqrt{10}x}$=$\frac{2}{5}$$\sqrt{10}$,
∴OA=$\frac{2}{5}$$\sqrt{10}$OF=$\frac{2}{5}$$\sqrt{10}$OE.
点评 本题考查了角平分线的性质,三角形全等的判定和性质,三角形相似的判定和性质,平行线分线段成比例定理以及勾股定理等,熟练掌握性质定理是解题的关键.

| A. | 画一条长3cm的射线 | B. | 延长射线OA到点C | ||
| C. | 直线、线段、射线中直线最长 | D. | 延长线段BA到C,使AC=BA |

| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
 如果有一个正方体,它的展开图可能是下列四个展开图中的( )
如果有一个正方体,它的展开图可能是下列四个展开图中的( )| A. |  | B. |  | C. |  | D. |  |
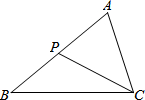 如图,点P为△ABC的AB边上一点(AB>AC),下列条件中不一定能保证△ACP∽△ABC的是( )
如图,点P为△ABC的AB边上一点(AB>AC),下列条件中不一定能保证△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{PC}{BC}$=$\frac{AC}{AB}$ | D. | $\frac{AC}{AB}$=$\frac{AP}{AC}$ |
 如图,在△ABC中,AB=AC,AC的垂直平分线分别交BC、AC于点D、E.
如图,在△ABC中,AB=AC,AC的垂直平分线分别交BC、AC于点D、E.