题目内容
3.若(-1,y1),(-2,y2),(-4,y3)在抛物线y=-2x2-8x+m上,则( )| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y2<y3<y1 |
分析 根据抛物线y=-2x2-8x+m上,可以求得该函数的对称轴,从而可以得到该函数的各点对应的函数值的大小,本题得以解决.
解答 解:∵抛物线y=-2x2-8x+m,
∴该抛物线的对称轴是直线x=$-\frac{-8}{2×(-2)}=-4$,
∴当x<-4时,y随x的增大而增大,当x>-4时,y随x的增大而减小,当x=-4时取得最大值,
∵(-1,y1),(-2,y2),(-4,y3)在抛物线y=-2x2-8x+m上,
∴y1<y2<y3,
故选A.
点评 本题考查二次函数图象上点的坐标特征,解答本题的关键是明确二次函数的图象,利用二次函数的性质解答.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
11.取15张扑克牌,其中6张“方块”,3张“梅花”,6张“红桃”,从中任抽一张,是“方块”或“红桃”的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{15}$ |
8.点(-3,2)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
15.估算$\sqrt{6}$的值( )
| A. | 在2.3到2.4之间 | B. | 在2.4到2.5之间 | C. | 在2.5到2.6之间 | D. | 在2.6到2.7之间 |
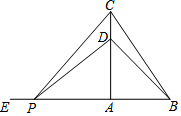 如图,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,点D在线段AC上,且CD=1 cm,动点P从BA的延长线上距A点5 cm的E点出发,以每秒2 cm的速度沿射线EA的方向运动了t秒.
如图,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,点D在线段AC上,且CD=1 cm,动点P从BA的延长线上距A点5 cm的E点出发,以每秒2 cm的速度沿射线EA的方向运动了t秒. 如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,用连线的方法,在图中按要求作图(保留作图痕迹,不写作法),在AB边上求一点N,连接CN,使CN=AM,并说明理由.
如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,用连线的方法,在图中按要求作图(保留作图痕迹,不写作法),在AB边上求一点N,连接CN,使CN=AM,并说明理由.