题目内容
 如图,在三角形ABC中,BD,CE分别为三角形ABC的高,连结DE,M,N分别为BC,DE中点.
如图,在三角形ABC中,BD,CE分别为三角形ABC的高,连结DE,M,N分别为BC,DE中点.(1)MN与DE有何位置关系?试说明理由;
(2)若DE=10,MN=2
| 14 |
(3)试探究当∠A为多少度时,三角形MDE为等边三角形.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质,等边三角形的判定
专题:
分析:(1)连接EM,DM,根据直角三角形斜边上的中线等于斜边的一半可得EM为BC的一半,DM也为BC的一半,推出EM=DM,根据等腰三角形的性质即可得出答案;
(2)根据勾股定理求出即可;
(3)由直角三角形斜边上的中线等于斜边的一半,求出EM=BM,CM=DM,根据三角形内角和定理求出∠ABC+∠ACB,即可求出∠EMD,根据等边三角形的判定得出即可.
(2)根据勾股定理求出即可;
(3)由直角三角形斜边上的中线等于斜边的一半,求出EM=BM,CM=DM,根据三角形内角和定理求出∠ABC+∠ACB,即可求出∠EMD,根据等边三角形的判定得出即可.
解答:解:(1)
MN⊥DE,
理由是:连接EM和DM,
∵BD,CE分别为三角形ABC的高,
∴∠BEC=∠BDC=90°,
∵M,N分别为BC,DE中点,
∴DM=
BC,EM=
BC,
∴EM=DM,
∵N为DE的中点,
∴MN⊥DE;
(2)∵DE=10,N为DE的中点,
∴DN=5,
∵MN=2
,
∴在Rt△DNM中,由勾股定理得:DM=
=9,
∴BC=2DM=18;
(3)∠A为60度时,三角形MDE为等边三角形,
理由是:∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠BEC=∠BDC=90°,M为BC的中点,
∴BM=EM,CM=DM,
∴∠ABC=∠BEM,∠ACB=∠CDM,
∴∠EMB+∠CMD=180°-∠ABC-∠BEC+180°-∠ACB-∠CDM=360°-120°-120°=120°,
∴∠EMD=180°-120°=60°,
∵EM=DM,
∴△EMD是等边三角形,
即∠A为60度时,三角形MDE为等边三角形.

MN⊥DE,
理由是:连接EM和DM,
∵BD,CE分别为三角形ABC的高,
∴∠BEC=∠BDC=90°,
∵M,N分别为BC,DE中点,
∴DM=
| 1 |
| 2 |
| 1 |
| 2 |
∴EM=DM,
∵N为DE的中点,
∴MN⊥DE;
(2)∵DE=10,N为DE的中点,
∴DN=5,
∵MN=2
| 14 |
∴在Rt△DNM中,由勾股定理得:DM=
| DN2+MN2 |
∴BC=2DM=18;
(3)∠A为60度时,三角形MDE为等边三角形,
理由是:∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠BEC=∠BDC=90°,M为BC的中点,
∴BM=EM,CM=DM,
∴∠ABC=∠BEM,∠ACB=∠CDM,
∴∠EMB+∠CMD=180°-∠ABC-∠BEC+180°-∠ACB-∠CDM=360°-120°-120°=120°,
∴∠EMD=180°-120°=60°,
∵EM=DM,
∴△EMD是等边三角形,
即∠A为60度时,三角形MDE为等边三角形.
点评:本题考查了等腰三角形的判定和性质,三角形内角和定理,勾股定理,直角三角形斜边上中线性质的应用,解此题的关键是正确作出辅助线,并求出EM=DM,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
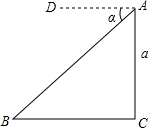 如图,飞机在空中A处探测得地面目标B处的俯角为α,此时飞机高度为AC=a,则BC的长度是( )
如图,飞机在空中A处探测得地面目标B处的俯角为α,此时飞机高度为AC=a,则BC的长度是( )| A、a•tanα | ||
B、
| ||
C、
| ||
D、
|
 如图所示的组合体,请画出它的三视图.
如图所示的组合体,请画出它的三视图. 如图,添加必要的一个条件,使得AB∥CD,这个条件可以是
如图,添加必要的一个条件,使得AB∥CD,这个条件可以是 如图,如果∠1=40°,∠2=40°,∠3=40°,可判定哪些直线平行,请说明所用的判定方法.
如图,如果∠1=40°,∠2=40°,∠3=40°,可判定哪些直线平行,请说明所用的判定方法.