Question

19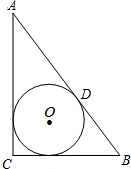．如图，⊙O为Rt△ABC的内切圆，切点D分斜边AB为两段，其中AD=10，BD=3，求AC和BC的长．

Answer 1

分析 设⊙O切AC于E，切BC于F，连接OE、OF，根据切线长定理得出AD=AE=10，BD=BF=3，CF=CE，得出∠OEC=∠C=∠OFC=90°，求出OE=CE=CF=OF，
设OE=R，由勾股定理得出（R+10）²+（R+3）²=（10+3）²，求出R，即可得出答案．

解答 解：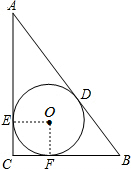
如图，设⊙O切AC于E，切BC于F，连接OE、OF，
∵⊙O为Rt△ABC的内切圆，AD=10，BD=3，
∴AD=AE=10，BD=BF=3，CF=CE，∠OEC=∠C=∠OFC=90°，
∴四边形OECF是正方形，
∴OE=CE=CF=OF，
设OE=R，由勾股定理得：AC²+BC²=AB²，
则（R+10）²+（R+3）²=（10+3）²，
∴R=2，
∴AC=2+10=12，BC=2+3=5．

点评 本题考查了三角形的内切圆，正方形的性质和判定，切线长定理，勾股定理的应用，能求出内切圆的半径是解此题的关键．