题目内容
5.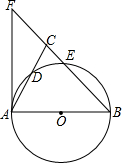 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
分析 (1)连接BD,由圆周角定理得出∠ADB=90°,由等腰三角形的性质得出∠ABC=2∠ABD,得出∠ABD=∠CAF,证出∠CAF+∠CAB=90°,BA⊥FA,即可得出结论;
(2)连接AE,由圆周角定理得出∠AEB=90°,设CE长为x,则EB长为3x,AB=BC=4x.由勾股定理可得AE=$\sqrt{7}x$,在Rt△AEC中,由勾股定理得出方程,解方程即可.
解答 (1)证明:连接BD,如图1所示:
∵AB是⊙O的直径
∴∠ADB=90°,
∵BA=BC,
∴BD平分∠ABC,即∠ABC=2∠ABD
∵∠ABC=2∠CAF,
∴∠ABD=∠CAF,
∵∠ABD+∠CAB=90°,
∴∠CAF+∠CAB=90°,即BA⊥FA,
∴AF是⊙O的切线;
(2)解:连接AE,如图2所示: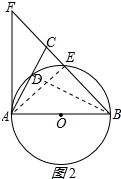
∵AB是⊙O的直径
∴∠AEB=90°,即△AEB为直角三角形,
∵CE:EB=1:3,
设CE长为x,则EB长为3x,BC长为4x.
则AB长为4x,
在Rt△AEB中由勾股定理可得 AE=$\sqrt{7}x$,
在Rt△AEC中,AC=4,AE=$\sqrt{7}x$,CE=x,
由勾股定理得:${4^2}={(\sqrt{7}x)^2}+{x^2}$,
解得:$x=±\sqrt{2}$,
∵x>0
∴$x=\sqrt{2}$,即CE长为$\sqrt{2}$.
点评 本题主要考查了切线的判定、勾股定理、圆周角定理、等腰三角形的性质;熟练掌握切线的判定方法,运用勾股定理得出方程是解决问题(2)的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
20.斜三角形ABC中,BE、CF是高,那么∠ABE和∠ACF的大小关系是( )
| A. | ∠ABE<∠ACF | B. | ∠ABE>∠ACF | C. | ∠ABE=∠ACF | D. | 不能确定 |




