题目内容
17.解方程组:$\left\{\begin{array}{l}{0.5x+0.7y=35}\\{x+0.4y=40}\end{array}\right.$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{5x+7y=350①}\\{5x+2y=200②}\end{array}\right.$,
①-②得:5y=150,即y=30,
把y=30代入①得:x=28,
则方程组的解为$\left\{\begin{array}{l}{x=28}\\{y=30}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
2.下列计算不正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-9)^{2}}$=$\sqrt{81}$=9 | ||
| C. | 9的算术平方根是3 | D. | 4的平方根是±2 |
7.已知二次函数y=a(x-1)2+3,当x<1时,y随x的增大而增大,则a取值范围是( )
| A. | a≥0 | B. | a≤0 | C. | a>0 | D. | a<0 |
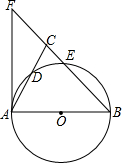 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.