题目内容
13.三棱柱有9条棱、6个顶点、5个面,三棱锥有6条棱、4个顶点、4个面;四棱柱有12条棱、8个顶点、6个面,四棱锥有8条棱、5个顶点、5个面等等,问能否组成一个有24条棱,10个面,15个顶点的多面体?请简要说明.分析 简单多面体的顶点数V、面数F及棱数E间的关系为:V+F-E=2.这个公式叫欧拉公式.依此即可求解.
解答 解:∵10+15-24=1,不符合欧拉公式V+F-E=2,
∴不能组成一个有24条棱,10个面,15个顶点的多面体.
点评 考查了欧拉公式,公式描述了简单多面体顶点数、面数、棱数特有的规律.解题的关键是熟练掌握欧拉公式.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.下列计算正确的是( )
| A. | (-5b)3=-15b3 | B. | (2x)3(-5xy2)=-40x4y2 | ||
| C. | 28x6y2+7x3y=4x2y | D. | (12a3-6a2+3a)÷3a=4a2-2a |
18.下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑩个图形中小圆圈的个数为( )


| A. | 24 | B. | 27 | C. | 30 | D. | 33 |
2.下列计算不正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-9)^{2}}$=$\sqrt{81}$=9 | ||
| C. | 9的算术平方根是3 | D. | 4的平方根是±2 |
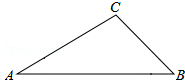 已知如图,在△ABC中,∠A=30°,∠C=105°,AC=$2\sqrt{3}$,求AB的长.
已知如图,在△ABC中,∠A=30°,∠C=105°,AC=$2\sqrt{3}$,求AB的长.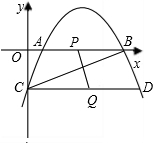 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴正半轴相交于点A(1,0)、B,与y轴相交于点C(0,-2).
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴正半轴相交于点A(1,0)、B,与y轴相交于点C(0,-2).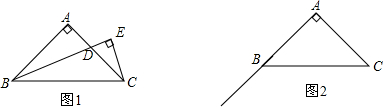
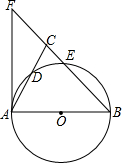 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF. 画出△ABC绕点C顺时针旋转90°后的图象△A′B′C.
画出△ABC绕点C顺时针旋转90°后的图象△A′B′C.