题目内容
14.平行四边形ABCD中,AB=6cm,AC+BD=14cm,则△DOC的周长为13cm.分析 由四边形ABCD是平行四边形,根据平行四边形的对边相等,对角线互相平分,可求得OC+OD与CD的长,继而求得答案.
解答  解:如图,∵四边形ABCD是平行四边形,
解:如图,∵四边形ABCD是平行四边形,
∴OC=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD,CD=AB=6cm,
∴OC+OD=$\frac{1}{2}$(AC+BD)=$\frac{1}{2}$×14=7(cm),
∴△DOC的周长为:CD+OC+OC=13(cm).
故答案为:13cm.
点评 此题考查了平行四边形的性质.注意平行四边形的对边相等,对角线互相平分.

练习册系列答案
相关题目
9.下面命题中,正确的是( )
| A. | 一组对角相等的四边形是平行四边形 | |
| B. | 一组对角互补的四边形是平行四边形 | |
| C. | 两组边分别相等的四边形是平行四边形 | |
| D. | 两组对角分别相等的四边形是平行四边形 |
6. 如图,是国际奥委会会旗上的图案,在该图案中反映出的两圆位置关系有( )
如图,是国际奥委会会旗上的图案,在该图案中反映出的两圆位置关系有( )
 如图,是国际奥委会会旗上的图案,在该图案中反映出的两圆位置关系有( )
如图,是国际奥委会会旗上的图案,在该图案中反映出的两圆位置关系有( )| A. | 内切、相交 | B. | 外离、内切 | C. | 外切、外离 | D. | 外离、相交 |
2.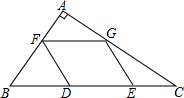 如图,在△ABC中,点D、E是BC边上的三等分点,点F在AB边上运动,点G在AC边上运动,在F、G运动过程中,若存在四边形FDEG是菱形,则△ABC必须满足的条件是( )
如图,在△ABC中,点D、E是BC边上的三等分点,点F在AB边上运动,点G在AC边上运动,在F、G运动过程中,若存在四边形FDEG是菱形,则△ABC必须满足的条件是( )
 如图,在△ABC中,点D、E是BC边上的三等分点,点F在AB边上运动,点G在AC边上运动,在F、G运动过程中,若存在四边形FDEG是菱形,则△ABC必须满足的条件是( )
如图,在△ABC中,点D、E是BC边上的三等分点,点F在AB边上运动,点G在AC边上运动,在F、G运动过程中,若存在四边形FDEG是菱形,则△ABC必须满足的条件是( )| A. | AB=AC且∠A=120° | B. | △ABC为正三角形 | ||
| C. | ∠A=90° | D. | 不存在这样的三角形 |
