题目内容
4. 如图,作菱形ABCD的高AE,E为CD的中点.AE=$\sqrt{3}$cm,则菱形ABCD的周长是( )
如图,作菱形ABCD的高AE,E为CD的中点.AE=$\sqrt{3}$cm,则菱形ABCD的周长是( )| A. | 4$\sqrt{3}$cm | B. | 4$\sqrt{2}$cm | C. | 4cm | D. | 8cm |
分析 通过解直角三角形ADE得到边AD的长度,然后由菱形的周长公式进行解答.
解答 解:在菱形ABCD中,AD=CD.
∵E为CD的中点,AE⊥CD,
∴ED=$\frac{1}{2}$CD=$\frac{1}{2}$AD,
∴∠DAE=30°,
∵AE=$\sqrt{3}$cm,
∴AD=$\frac{AE}{cos30°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2(cm),
∴菱形ABCD的周长=4AD=8cm.
故选:D.
点评 本题考查了菱形的性质.解题时,利用了菱形的四条边相等的性质.

练习册系列答案
相关题目
9.已知方程组$\left\{\begin{array}{l}{2x+y=3k-2}\\{x+2y=-k+1}\end{array}\right.$的解满足x-y≥5,则K可取的值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 3 |
16.投掷一枚质地均匀的骰子一次,正面是偶数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
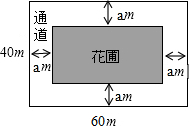 如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.
如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.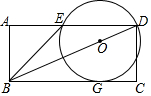 如图,矩形ABCD的一边BC与⊙O相切于G,DC=6,且对角线BD经过圆心O,AD交⊙O于点E,连接BE,BE恰好是⊙O的切线,已知点P在对角线BD上运动,若以B、P、G三点构成的三角形与△BED相似,则BP=4或12.
如图,矩形ABCD的一边BC与⊙O相切于G,DC=6,且对角线BD经过圆心O,AD交⊙O于点E,连接BE,BE恰好是⊙O的切线,已知点P在对角线BD上运动,若以B、P、G三点构成的三角形与△BED相似,则BP=4或12.