题目内容
9．已知函数y=（k-2）xk2-4k+5+2x是关于x的二次函数．求：（1）满足条件的k的值；
（2）当k为何值时，抛物线有最高点？求出这个最高点，这时，x为何值时，y随x的增大而增大？
分析 （1）根据二次函数的指数是二，可得方程，根据解方程，可得答案；
（2）根据函数有最大值，可得二次项系数是负数，根据顶点坐标是函数的最值，可得答案；根据a＜0时，对称轴的左侧y随x的增大而增大，可得答案．
解答 解：（1）函数y=（k-2）xk2-4k+5+2x是关于x的二次函数，得
$\left\{\begin{array}{l}{{k}^{2}-4k+5=2}\\{k-2≠0}\end{array}\right.$，
解得k=1或k=3；
（2）当k=1时，函数y=-x2+2x有最高点；
y=-（x-1）2+1，
最高点的坐标为（1，1），
当x＜1时，y随x的增大而增大．
点评 本题考查了二次函数的定义，利用二次函数的定义得出k值是解题关键，又利用了二次函数的性质．
练习册系列答案
相关题目
如图，OA=OB，OC=OD，∠O=60°，∠C=25°，则∠OAD等于95度．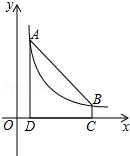
如图，点A（m，6），B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C．
结合数轴与绝对值的知识回答下列问题：