题目内容
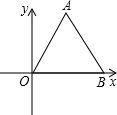 如图,△AOB是边长为6的等边三角形,则OA所在直线方程为
如图,△AOB是边长为6的等边三角形,则OA所在直线方程为考点:待定系数法求一次函数解析式,等边三角形的性质
专题:计算题
分析:作AC⊥OB于C,根据等边三角形的性质得AO=6,OC=3,再利用勾股定理计算出AC=3
,则A点坐标为(3,3),然后利用待定系数法确定直线OA的解析式.
| 3 |
解答:解:作AC⊥OB于C,如图,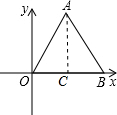
∵△AOB是边长为6的等边三角形,
∴AO=6,OC=3,
∴AC=
=3
,
∴A点坐标为(3,3),
设直线OA的解析式为y=kx,
把A(3,3
)代入得3k=3
,解得k=
,
∴直线OA的解析式为y=
x.
故答案为y=
x.

∵△AOB是边长为6的等边三角形,
∴AO=6,OC=3,
∴AC=
| OA2-OC2 |
| 3 |
∴A点坐标为(3,3),
设直线OA的解析式为y=kx,
把A(3,3
| 3 |
| 3 |
| 3 |
∴直线OA的解析式为y=
| 3 |
故答案为y=
| 3 |
点评:本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.也考查了等边三角形的性质.

练习册系列答案
相关题目
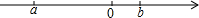 实数a、b在数轴上的位置如图所示,给出如下结论:①a+b>0;②b-a>0;③-a>b;④a>-b,⑤|a|>|b|>0.其中正确的结论是( )
实数a、b在数轴上的位置如图所示,给出如下结论:①a+b>0;②b-a>0;③-a>b;④a>-b,⑤|a|>|b|>0.其中正确的结论是( )| A、①②③ | B、②③④ |
| C、②③⑤ | D、②④⑤ |
已知a-b=5,ab=3,则a2+b2的值是( )
| A、25 | B、28 | C、30 | D、31 |
下列长度的三条线段能组成三角形的是( )
| A、6,8,10 |
| B、4,5,9 |
| C、1,2,4 |
| D、5,15,8 |
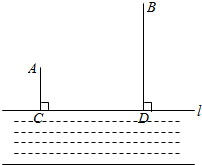 如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为
如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为