题目内容
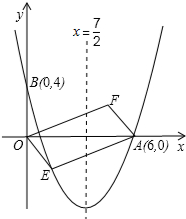 如图,对称轴为直线x=
如图,对称轴为直线x=| 7 |
| 2 |
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
考点:二次函数综合题
专题:
分析:(1)根据对称轴为直线x=
的抛物线经过点A(6,0)和B(0,4),设所求抛物线的解析式为y=a(x-
)2+b,代入A、B坐标求出解析式,然后求得顶点坐标;
(2)由设点E(x,y)是抛物线上一动点,且位于第四象限,可得y<0,即-y>0,-y表示点E到OA的距离,又由S=2S△OAE=2×
×OA•|y|,即可求得平行四边形OEAF的面积S与x之间的函数关系式,结合图象,求得自变量x的取值范围;
(3)由平行四边形OEAF的面积为24,可得方程:-4x2+28x-24=24,解此方程可求得E点坐标,然后分析OE与AE的关系,即可判定平行四边形OEAF是否为菱形.
| 7 |
| 2 |
| 7 |
| 2 |
(2)由设点E(x,y)是抛物线上一动点,且位于第四象限,可得y<0,即-y>0,-y表示点E到OA的距离,又由S=2S△OAE=2×
| 1 |
| 2 |
(3)由平行四边形OEAF的面积为24,可得方程:-4x2+28x-24=24,解此方程可求得E点坐标,然后分析OE与AE的关系,即可判定平行四边形OEAF是否为菱形.
解答:解:(1)∵对称轴为直线x=
,
设所求抛物线的解析式为y=a(x-
)2+b,
则由题意可得:
,
解得:
,
∴所求抛物线的解析式为:y=
(x-
)2-
=
x2-
x+4,
顶点坐标为:(
,-
);
(2)∵点E(x,y)在抛物线上,位于第四象限,且坐标适合y=
x2-
x+4,
∴y<0,
即-y>0,-y表示点E到OA的距离.
∵OA是平行四边形OEAF的对角线,
∴S=2S△OAE=2×
×OA•|y|=-6y=-6(
x2-
x+4)=-4x2+28x-24,
自变量x的取值范围为:1<x<6;
(3)根据题意得:-4x2+28x-24=24,
解得x1=3,x2=4,
∴所求的点E有两个,分别为E1(3,-4),E2(4,-4),
∵点E1(3,-4),
∴OE=5,AE=
=5,
∴OE=AE,
∴平行四边形OEAF是菱形,
∵点E2(4,-4),
∴OE=4
,AE=
=2
,
∴不满足OE=AE,
∴平行四边形OEAF不是菱形,
综上所述,当点E坐标为(3,-4)时,平行四边形OEAF为菱形.
| 7 |
| 2 |
设所求抛物线的解析式为y=a(x-
| 7 |
| 2 |
则由题意可得:
|
解得:
|
∴所求抛物线的解析式为:y=
| 2 |
| 3 |
| 7 |
| 2 |
| 25 |
| 6 |
| 2 |
| 3 |
| 14 |
| 3 |
顶点坐标为:(
| 7 |
| 2 |
| 25 |
| 6 |
(2)∵点E(x,y)在抛物线上,位于第四象限,且坐标适合y=
| 2 |
| 3 |
| 14 |
| 3 |
∴y<0,
即-y>0,-y表示点E到OA的距离.
∵OA是平行四边形OEAF的对角线,
∴S=2S△OAE=2×
| 1 |
| 2 |
| 2 |
| 3 |
| 14 |
| 3 |
自变量x的取值范围为:1<x<6;
(3)根据题意得:-4x2+28x-24=24,
解得x1=3,x2=4,
∴所求的点E有两个,分别为E1(3,-4),E2(4,-4),
∵点E1(3,-4),
∴OE=5,AE=
| (3-6)2+(-4-0)2 |
∴OE=AE,
∴平行四边形OEAF是菱形,
∵点E2(4,-4),
∴OE=4
| 2 |
| (4-6)2+(-4-0)2 |
| 5 |
∴不满足OE=AE,
∴平行四边形OEAF不是菱形,
综上所述,当点E坐标为(3,-4)时,平行四边形OEAF为菱形.
点评:此题属于二次函数综合题,考查了待定系数法求二次函数的解析式、配方法求顶点坐标、平行四边形的性质、菱形的判定以及正方形的判定等知识.此题综合性很强,难度较大,注意数形结合思想、方程思想与函数思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
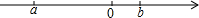 实数a、b在数轴上的位置如图所示,给出如下结论:①a+b>0;②b-a>0;③-a>b;④a>-b,⑤|a|>|b|>0.其中正确的结论是( )
实数a、b在数轴上的位置如图所示,给出如下结论:①a+b>0;②b-a>0;③-a>b;④a>-b,⑤|a|>|b|>0.其中正确的结论是( )| A、①②③ | B、②③④ |
| C、②③⑤ | D、②④⑤ |
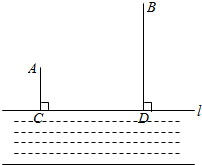 如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为
如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为 如图,线段AB上两点C、D,AB=30cm,AC=10cm,BD=5cm,点P从A出发以每秒1cm的速度,沿A→C→D→B→D运动,点Q从B出发,沿B→D→C→A→C运动,P,Q两点运动到终点D,C后停止运动,当Q到达D点时,PA=
如图,线段AB上两点C、D,AB=30cm,AC=10cm,BD=5cm,点P从A出发以每秒1cm的速度,沿A→C→D→B→D运动,点Q从B出发,沿B→D→C→A→C运动,P,Q两点运动到终点D,C后停止运动,当Q到达D点时,PA=