题目内容
 在△ABC中,BC=AC,∠C=90°,AC=7cm,AD是∠BAC的平分线,DE⊥AB于E,求△DEB的周长.
在△ABC中,BC=AC,∠C=90°,AC=7cm,AD是∠BAC的平分线,DE⊥AB于E,求△DEB的周长.考点:角平分线的性质,等腰直角三角形
专题:
分析:根据角平分线上的点到角的两边的距离相等可得CD=ED,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AE=AC,然后求出△DEB的周长=AB,在等腰直角三角形ABC中由勾股定理求出AB即可得解.
解答:解:∵AD是∠BAC的平分线,DE⊥AB于E,∠C=90°,
∴CD=ED.
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
又∵AC=BC,
∴△DEB的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB,
∵在△ABC中,BC=AC,∠C=90°,AC=7cm,
∴AB=7
cm,
∴△DEB的周长=7
cm.
∴CD=ED.
在Rt△ACD和Rt△AED中,
|
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
又∵AC=BC,
∴△DEB的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB,
∵在△ABC中,BC=AC,∠C=90°,AC=7cm,
∴AB=7
| 2 |
∴△DEB的周长=7
| 2 |
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,勾股定理,难度适中,求出△DEB的周长=AB是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在△ABC中,∠A=150°,AB=AC=6cm,求△ABC的面积.
如图,在△ABC中,∠A=150°,AB=AC=6cm,求△ABC的面积. 如图,△ABC为等边三角形,D是AC的中点,E是BC延长线上一点,且CE=
如图,△ABC为等边三角形,D是AC的中点,E是BC延长线上一点,且CE=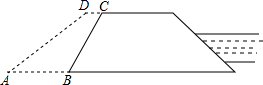 由于发生大洪水,需要加固一段大堤,计划使大堤加宽1m,使坡度由原来的1:2变成1:3.已知原来BC=12m,堤长100m,那么需要砂石和土多少立方米?
由于发生大洪水,需要加固一段大堤,计划使大堤加宽1m,使坡度由原来的1:2变成1:3.已知原来BC=12m,堤长100m,那么需要砂石和土多少立方米?