题目内容
对于任意的正整数n，代数式n（n+7）-（n+3）（n-2）的值是否总能被6整除，请说明理由．
考点：整式的混合运算
专题：
分析：先算乘法，再合并同类项，最后除以6得出结果，即可判断答案．
解答：解：能，
理由是：n（n+7）-（n+3）（n-2）
=n2+7n-n2+2n-3n+6
=6n+6，
（6n+6）÷6=n+1，
∵n为正整数，
∴n+1是正整数，
∴对于任意的正整数n，代数式n（n+7）-（n+3）（n-2）的值总能被6整除．
理由是：n（n+7）-（n+3）（n-2）
=n2+7n-n2+2n-3n+6
=6n+6，
（6n+6）÷6=n+1，
∵n为正整数，
∴n+1是正整数，
∴对于任意的正整数n，代数式n（n+7）-（n+3）（n-2）的值总能被6整除．
点评：本题考查了整式的混合运算的应用，主要考查学生的计算能力和理解能力，题目比较好，难度适中．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
下列每一组数据中的三个数值分别为三角形的三边长，不能构成直角三角形的是（ ）
| A、3、4、5 |
| B、6、8、10 |
| C、4、2、9 |
| D、5、12、13 |
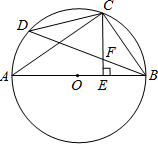如图，AB是⊙O的直径，C是弧BD的中点，CE⊥AB于E，BD交CE于点F．△ABC中，AB=AC，∠A=40°，BD是高，则∠DBC=（ ）
| A、40° | B、20° |
| C、70° | D、35° |
