题目内容
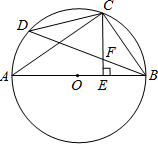 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB于E,BD交CE于点F.
如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB于E,BD交CE于点F.(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的直径AB和线段CE的长.
考点:圆周角定理,勾股定理
专题:
分析:(1)首先延长CE交⊙O于点M,由CE⊥AB,根据垂径定理即可得
=
,又由C是弧BD的中点,即可证得
=
,然后由圆周角定理,证得∠1=∠2,即可证得CF=BF;
(2)由C是弧BD的中点,可得BC=CD=6,又由AB是⊙O的直径,即可证得∠ACB=90°,然后由勾股定理求得AB的长,然后利用三角形的面积,求得高CE的长.
 |
| BC |
 |
| BM |
 |
| CD |
 |
| BM |
(2)由C是弧BD的中点,可得BC=CD=6,又由AB是⊙O的直径,即可证得∠ACB=90°,然后由勾股定理求得AB的长,然后利用三角形的面积,求得高CE的长.
解答: (1)证明:延长CE交⊙O于点M,
(1)证明:延长CE交⊙O于点M,
∵CE⊥AB,
∴
=
,
∵C是弧BD的中点,
∴
=
,
∴
=
,
∴∠1=∠2,
∴CF=BF;
(2)解:∵C是弧BD的中点,
∴BC=CD=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB=
=
=10,
∵CE⊥AB,
∴CE=
=4.8.
 (1)证明:延长CE交⊙O于点M,
(1)证明:延长CE交⊙O于点M,∵CE⊥AB,
∴
 |
| BC |
 |
| BM |
∵C是弧BD的中点,
∴
 |
| CD |
 |
| BC |
∴
 |
| CD |
 |
| BM |
∴∠1=∠2,
∴CF=BF;
(2)解:∵C是弧BD的中点,
∴BC=CD=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB=
| AC2+BC2 |
| 82+62 |
∵CE⊥AB,
∴CE=
| AC•BC |
| AB |
点评:此题考查了圆周角定理、垂径定理、等腰三角形的判定以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
格兰仕微波炉原来每台售价a 元现降价25%后每台售价( )
| A、0.25a元 | ||
B、
| ||
| C、0.75a元 | ||
D、
|
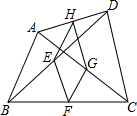 如图,在四边形ABCD中,点E,F,G,H分别是边BD,BC,AC,DA的中点,如果四边形EFGH为矩形,那么应在四边形ABCD中添加一个条件
如图,在四边形ABCD中,点E,F,G,H分别是边BD,BC,AC,DA的中点,如果四边形EFGH为矩形,那么应在四边形ABCD中添加一个条件