题目内容
6. 如图,在在平面直角坐标系中,四边形ABCD是梯形,AD∥BC,E是BC的中点,BC=12,点A坐标是(0,4),CD所在直线的函数关系式为y=-x+9,点P是BC边上一个动点,
如图,在在平面直角坐标系中,四边形ABCD是梯形,AD∥BC,E是BC的中点,BC=12,点A坐标是(0,4),CD所在直线的函数关系式为y=-x+9,点P是BC边上一个动点,(1)当PB=1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(2)在(1)的条件下,点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
分析 (1)若以点P、A、D、E为顶点的四边形为平行四边形,则AD=PE,有两种情况:①当P在E的左边,利用已知条件可以求出BP的长度;②当P在E的右边,利用已知条件也可求出BP的长度;
(2)以点P、A、D、E为顶点的四边形能构成菱形.由(1)知,当BP=11时,以点P、A、D、E为顶点的四边形是平行四边形,根据已知条件分别计算一组邻边,证明它们相等即可证明是菱形.
解答 解:(1)∵AD∥BC,点A坐标是(0,4),CD所在直线的函数关系式为y=-x+9,
∴OC=9,D点的纵坐标为4,D点的横坐标为5,
作DN⊥BC交于N,如图1所示:
则四边形OADN为矩形,
∴CN=OC-ON=OC-AD=9-5=4,DF=4,
∴△DFC为等腰直角三角形,
∴CD=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
若以点P、A、D、E为顶点的四边形为平行四边形,则AD=PE=5,
有两种情况:①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE-PE=6-5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当BP=1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(2)①当BP=1时,此时CN=DN=4,NE=6-4=2,
∴DE=$\sqrt{D{N}^{2}+N{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$≠AD,故不能构成菱形.
②当BP′=11时,以点P′、A、D、E为顶点的四边形是平行四边形
∴EP′=AD=5,
过D作DN⊥BC于N,如图2所示:
由(1)得:DN=CN=4,
∴NP′=BP′-BN=BP′-(BC-CN)=11-(12-4)=3.
∴DP′=$\sqrt{D{N}^{2}+NP{′}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴EP′=DP′,
故此时平行四边形P′DAE是菱形,
即以点P、A、D、E为顶点的四边形能构成菱形.
点评 本题是四边形综合题目,考查了等腰直角三角形的判定与性质、勾股定理、平行四边形的判定、矩形的判定、菱形的判定等知识;本题综合性强,难度较大,需要进行分类讨论.

| A. | y=$\frac{1}{9x}$ | B. | $\frac{y}{2x}=1$ | C. | y=-3x2 | D. | $\frac{1}{5}$xy=-2 |
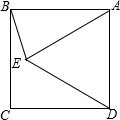 如图,在正方形ABCD的内部作等边△ADE,则∠AEB度数为( )
如图,在正方形ABCD的内部作等边△ADE,则∠AEB度数为( )| A. | 80° | B. | 75° | C. | 70° | D. | 60° |
| A. | m+$\frac{5}{2}$>0 | B. | $\frac{1}{2}$(m+5)≥0 | C. | $\frac{1}{2}$(m+5)>0 | D. | $\frac{1}{2}$(m+5)<0 |
| A. | k$≤-\frac{9}{4}$ | B. | k$≥-\frac{9}{4}$且k≠0 | C. | k$≥-\frac{9}{4}$ | D. | k>$-\frac{9}{4}$且k≠0 |