题目内容
17．
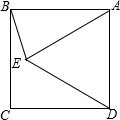如图，在正方形ABCD的内部作等边△ADE，则∠AEB度数为（ ）| A． | 80° | B． | 75° | C． | 70° | D． | 60° |
分析 由正方形和等边三角形的性质得出AB=AE，∠BAE=30°，由等腰三角形的性质和三角形内角和定理即可得出结果．
解答 解：∵四边形ABCD是正方形，
∴∠BAD=90°，AB=AD，
∵△ADE是等边三角形，
∴∠DAE=60°，AE=AD，
∴AB=AE，∠BAE=90°-60°=30°，
∴∠AEB=$\frac{1}{2}$（180°-30°）=75°；
故选：B．
点评 本题考查了正方形的性质、等边三角形的性质、等腰三角形的性质、三角形内角和定理；熟练掌握正方形和等边三角形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
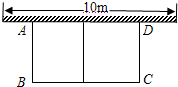如图，一面利用墙，用总长度为24m的篱笆围成矩形花圃ABCD，其中中间用一段篱笆隔成两个小矩形，墙可利用的最大长度为10m，设AB的长为xm，矩形花圃ABCD的面积为ym2．
如图，破残的圆形轮片上，弦AB的垂直平分线交弧AB于C，交弦AB于D．求作此残片所在的圆（不写作法，保留作图痕迹）．
5．比较$\sqrt{2}$和$\frac{\sqrt{5}}{2}$的大小（ ）
| A． | $\sqrt{2}$≥$\frac{\sqrt{5}}{2}$ | B． | $\sqrt{2}$≤$\frac{\sqrt{5}}{2}$ | C． | $\sqrt{2}$＞$\frac{\sqrt{5}}{2}$ | D． | $\sqrt{2}$＜$\frac{\sqrt{5}}{2}$ |
如图，在在平面直角坐标系中，四边形ABCD是梯形，AD∥BC，E是BC的中点，BC=12，点A坐标是（0，4），CD所在直线的函数关系式为y=-x+9，点P是BC边上一个动点，