题目内容
3.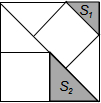 有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )| A. | 1:$\sqrt{2}$ | B. | 1:2 | C. | 2:3 | D. | 4:9 |
分析 根据题意先求出EF=$\frac{1}{3}$AC,再根据$\frac{CG}{AC}$=$\frac{1}{2}$,求出CG=$\frac{1}{2}$AC,从而得出$\frac{EF}{CG}$,再根据相似比即可得出S1:S2的比值.
解答 解:∵四边形EFNM是正方形,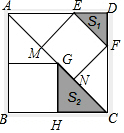
∴EF=MN,
∴$\frac{EF}{AC}$=$\frac{1}{3}$,
∴EF=$\frac{1}{3}$AC,
∵$\frac{CG}{AC}$=$\frac{1}{2}$,
∴CG=$\frac{1}{2}$AC,
∴$\frac{EF}{CG}$=$\frac{\frac{1}{3}AC}{\frac{1}{2}AC}$=$\frac{2}{3}$,
易证:△DEF∽△HCG,
∴S1:S2=4:9;
故选D.
点评 此题考查了正方形的性质,用到的知识点是正方形的性质、相似三角形的性质、正方形的面积公式,关键是根据题意求出$\frac{EF}{CG}$的比值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.为调查聊城市某村开展“要致富,多读书”活动的效果,小红利用周末随机抽查了该村部分村民在一周内的阅读时间,并将结果绘制成如图两幅不完整的统计图,则本次调查的阅读时间的中位数和众数分别为( )
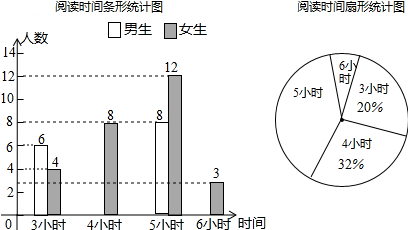

| A. | 4小时,5小时 | B. | 5小时,4小时 | C. | 4小时,4小时 | D. | 5小时,5小时 |
14.已知等腰三角形的周长等于20,那么底边长y与腰长x的函数解析式和定义域分别是( )
| A. | y=20-2x(0<x<20) | B. | y=20-2x(0<x<10) | C. | y=20-2x(5<x<10) | D. | y=$\frac{20-x}{2}$(5<x<10) |
18.下列等式正确的是( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{CB}$+$\overrightarrow{BA}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{AC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BC}$-$\overrightarrow{AC}$=$\overrightarrow{0}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{DA}$ |
12.甲、乙、丙3人聚会,每人带了一件从外盒包装上看完全相同的礼物(里面的东西只有颜色不同),将3件礼物放在一起,每人从中随机抽取一件.则下列事件是必然事件的是( )
| A. | 乙抽到一件礼物 | B. | 乙恰好抽到自己带来的礼物 | ||
| C. | 乙没有抽到自己带来的礼物 | D. | 只有乙抽到自己带来的礼物 |
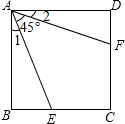 如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论: