题目内容
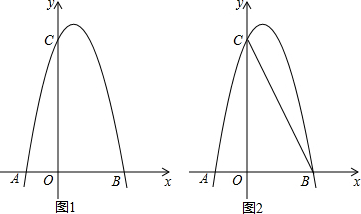
15.如图1,对称轴为直线x=$\frac{1}{2}$的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
分析 (1)由对称轴的对称性得出点A的坐标,由待定系数法求出抛物线的解析式;
(2)作辅助线把四边形COBP分成梯形和直角三角形,表示出面积S,化简后是一个关于S的二次函数,求最值即可;
(3)画出符合条件的Q点,只有一种,①利用平行相似得对应高的比和对应边的比相等列比例式;②在直角△OCQ和直角△CQM利用勾股定理列方程;两方程式组成方程组求解并取舍.
解答 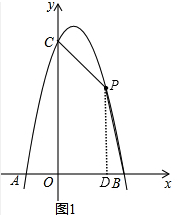 解:(1)由对称性得:A(-1,0),
解:(1)由对称性得:A(-1,0),
设抛物线的解析式为:y=a(x+1)(x-2),
把C(0,4)代入:4=-2a,
a=-2,
∴y=-2(x+1)(x-2),
∴抛物线的解析式为:y=-2x2+2x+4;
(2)如图1,设点P(m,-2m2+2m+4),过P作PD⊥x轴,垂足为D,
∴S=S梯形+S△PDB=$\frac{1}{2}$m(-2m2+2m+4+4)+$\frac{1}{2}$(-2m2+2m+4)(2-m),
S=-2m2+4m+4=-2(m-1)2+6,
∵-2<0,
∴S有最大值,则S大=6;
(3)存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形,
理由是:
分以下两种情况:
①当∠BQM=90°时,如图2:
∵∠CMQ>90°,
∴只能CM=MQ.
设直线BC的解析式为:y=kx+b(k≠0),
把B(2,0)、C(0,4)代入得:$\left\{\begin{array}{l}{2k+b=0}\\{b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$,
∴直线BC的解析式为:y=-2x+4,
设M(m,-2m+4),
则MQ=-2m+4,OQ=m,BQ=2-m,
在Rt△OBC中,BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵MQ∥OC,
∴△BMQ∽BCO,
∴$\frac{BM}{BC}=\frac{BQ}{BO}$,即$\frac{BM}{2\sqrt{5}}=\frac{2-m}{2}$,
∴BM=$\sqrt{5}$(2-m)=2$\sqrt{5}$-$\sqrt{5}$m,
∴CM=BC-BM=2$\sqrt{5}$-(2$\sqrt{5}$-$\sqrt{5}$m)=$\sqrt{5}$m,
∵CM=MQ,
∴-2m+4=$\sqrt{5}$m,m=$\frac{4}{\sqrt{5}+2}$=4$\sqrt{5}$-8.
∴Q(4$\sqrt{5}$-8,0).
②当∠QMB=90°时,如图3,
同理可设M(m,-2m+4),
过A作AE⊥BC,垂足为E,
∴∠EAB=∠OCB,
∴sin∠EAB=$\frac{BE}{AB}=\frac{OB}{BC}$,
∴$\frac{BE}{3}=\frac{2}{2\sqrt{5}}$,
∴BE=$\frac{3\sqrt{5}}{5}$,
过E作EF⊥x轴于F,
sin∠CBO=$\frac{EF}{BE}=\frac{OC}{BC}$,
∴$\frac{EF}{\frac{3\sqrt{5}}{5}}=\frac{4}{2\sqrt{5}}$,
∴EF=$\frac{6}{5}$,
由勾股定理得:BF=$\sqrt{B{E}^{2}-E{F}^{2}}$=$\frac{3}{5}$,
∴OF=2-$\frac{3}{5}$=$\frac{7}{5}$,
∴E($\frac{7}{5}$,$\frac{6}{5}$),
由A(-1,0)和E($\frac{7}{5}$,$\frac{6}{5}$)可得:
则AE的解析式为:y=$\frac{1}{2}$x+$\frac{1}{2}$,
则直线BC与直线AE的交点E(1.4,1.2),
设Q(-x,0)(x>0),
∵AE∥QM,
∴△ABE∽△QBM,
∴$\frac{1.2}{-2m+4}=\frac{3}{2+x}$①,
由勾股定理得:x2+42=2×[m2+(-2m+4-4)2]②,
由以上两式得:m1=4(舍),m2=$\frac{4}{3}$,
当m=$\frac{4}{3}$时,x=$\frac{4}{3}$,
∴Q(-$\frac{4}{3}$,0).
综上所述,Q点坐标为(4$\sqrt{5}$-8,0)或(-$\frac{4}{3}$,0).
点评 本题是二次函数的综合问题,综合性较强;考查了利用待定系数法求二次函数和一次函数的解析式,并利用方程组求图象的交点坐标,将函数和方程有机地结合,进一步把函数简单化;同时还考查了相似的性质:在二次函数的问题中,如果利用勾股定理不能求的边可以考虑利用相似的性质求解.

 阅读快车系列答案
阅读快车系列答案| A. | 两个有理数的和是无理数 | |
| B. | 从装有5个红球和1个白球的袋子中随机摸出1球是白球 | |
| C. | 买一张电影票,座位号是偶数 | |
| D. | 购买1张彩票中奖 |
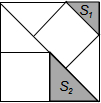 有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )| A. | 1:$\sqrt{2}$ | B. | 1:2 | C. | 2:3 | D. | 4:9 |
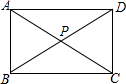 如图,已知四边形ABCD是矩形,对角线AC,BD交于点P,则下列结论正确的是( )
如图,已知四边形ABCD是矩形,对角线AC,BD交于点P,则下列结论正确的是( )| A. | AC是∠BAD的平分线 | B. | AC⊥BD | ||
| C. | AC=BD | D. | AC>2BP |
| 型号 | A | B | C | D | E |
| 数量(双) | 3 | 8 | 22 | 10 | 4 |
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
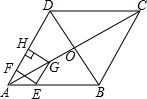 如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒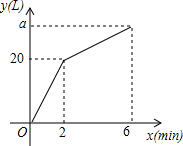 一个容器装有一个注水管和两个排水管,每个排水管每分钟排水7.5L,从某一时刻开始2min内只注水不排水,2min后开启一个排水管,容器内的水量y(L)与注水时间x(min)之间的函数关系如图所示.
一个容器装有一个注水管和两个排水管,每个排水管每分钟排水7.5L,从某一时刻开始2min内只注水不排水,2min后开启一个排水管,容器内的水量y(L)与注水时间x(min)之间的函数关系如图所示.