题目内容
4.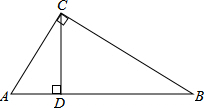 在△ABC中,∠C=90°,∠B=30°,AC=5$\sqrt{2}$,BC=5$\sqrt{6}$,CD⊥AB于点D.
在△ABC中,∠C=90°,∠B=30°,AC=5$\sqrt{2}$,BC=5$\sqrt{6}$,CD⊥AB于点D.(1)求CD的长;
(2)若以AC边为对称轴,作△ABC的对称图形,得到△AB′C,点B与B′为对应点,求△AB′B的面积.
分析 (1)根据CD⊥AB,∠B=30°,可得Rt△BCD中,CD=$\frac{1}{2}$BC;
(2)根据轴对称变换,得到点B'的位置,进而得到△AB′C,根据△ABB'为等腰三角形,即可得到△AB′B的面积.
解答 解:(1)∵CD⊥AB,BC=5$\sqrt{6}$,∠B=30°,
∴Rt△BCD中,CD=$\frac{1}{2}$BC=$\frac{5}{2}\sqrt{6}$;
(2)如图所示,△AB′C即为所求;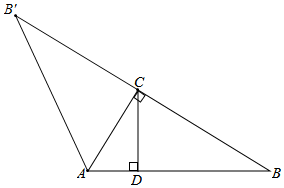
由轴对称的性质可得,B'C=BC=5$\sqrt{6}$,∠BCB'=180°,
∴BB'=10$\sqrt{6}$,
∴△AB′B的面积=$\frac{1}{2}$BB'×AC=$\frac{1}{2}$×10$\sqrt{6}$×5$\sqrt{2}$=50$\sqrt{3}$.
点评 本题主要考查了利用轴对称变换进行作图,含30°角直角三角形的性质以及三角形面积的计算,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
2.关于x的方程x2+6x+a=0的左边是完全平方式,则a的值为( )
| A. | 9 | B. | 12 | C. | 36 | D. | 144 |
20.若x-2y的值是3,则1-2x+4y的值是( )
| A. | 7 | B. | 5 | C. | 1 | D. | -5 |
13.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{(-2)^{2}}$=2 | C. | $\sqrt{27}$=3 | D. | $\frac{1}{\sqrt{3}}$=$\sqrt{3}$ |
14.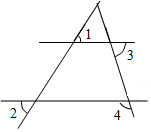 如图所示,若∠1=∠2=45°,∠3=70°,则∠4等于( )
如图所示,若∠1=∠2=45°,∠3=70°,则∠4等于( )
 如图所示,若∠1=∠2=45°,∠3=70°,则∠4等于( )
如图所示,若∠1=∠2=45°,∠3=70°,则∠4等于( )| A. | 70° | B. | 45° | C. | 110° | D. | 135° |
