题目内容
12. 如图,已知AB,CD相交于点O,F是AC的中点,OA=OC,∠1=∠2,求证:
如图,已知AB,CD相交于点O,F是AC的中点,OA=OC,∠1=∠2,求证:(1)OB=OD;
(2)AC∥BD.
分析 (1)利用已知条件证明△AFB≌△CFD,得到FB=FD,利用等边对等角得到∠FDB=∠FBD,再证明∠ODB=∠OBD,即可得到OB=OD.
(2)根据三角形的内角和为180°,对顶角相等,得到∠ODB+∠OBD=∠A+∠C,由∠A=∠C,∠ODB=∠OBD,即可得到∠ODB=∠C,所以AC∥BD.
解答 解:(1)∵OA=OC,
∴∠A=∠C,
∵F是AC的中点,
∴AF=CF,
在△AFB和△CFD中,
$\left\{\begin{array}{l}{∠A=∠C}\\{∠1=∠2}\\{AF=CF}\end{array}\right.$
∴△AFB≌△CFD,
∴FB=FD,
∴∠FDB=∠FBD,
∵∠1=∠2,
∴∠FDB-∠1=∠FBD-∠2,
∴∠ODB=∠OBD,
∴OB=OD.
(2)∵∠ODB+∠OBD+∠BOD=180°,∠A+∠C+∠COA=180°,∠BOD=∠COA,
∴∠ODB+∠OBD=∠A+∠C,
∵∠A=∠C,∠ODB=∠OBD,
∴2∠ODB=2∠C,
∴∠ODB=∠C,
∴AC∥BD.
点评 本题考查了全等三角形的性质与判定,解决本题的根据是证明△AFB≌△CFD,得到相等的边.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
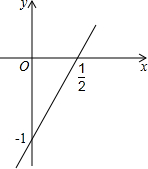 已知函数y=2x-1的图象如图所示,请根据图象回答下列问题:
已知函数y=2x-1的图象如图所示,请根据图象回答下列问题: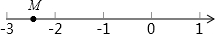 在数轴上,点M的位置如图所示,设点M表示有理数m,点P表示m的相反数,点Q表示m的倒数,点N表示m的绝对值,点R表示m的平方.则这些点中,一定与M位于原点同侧的点是( )
在数轴上,点M的位置如图所示,设点M表示有理数m,点P表示m的相反数,点Q表示m的倒数,点N表示m的绝对值,点R表示m的平方.则这些点中,一定与M位于原点同侧的点是( ) 如图,在?ABCD中,以A为圆心,以AB为半径作圆交AD于F,交BC于G,BA的延长线交⊙A于E,求证:$\widehat{EF}$=$\widehat{FG}$.
如图,在?ABCD中,以A为圆心,以AB为半径作圆交AD于F,交BC于G,BA的延长线交⊙A于E,求证:$\widehat{EF}$=$\widehat{FG}$.