题目内容
17.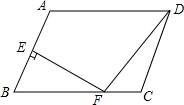 在?ABCD中,AB=12,AD=16,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为4$\sqrt{13}$.
在?ABCD中,AB=12,AD=16,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为4$\sqrt{13}$.
分析 首先延长DC,EF相交于点H.由在?ABCD中,AB=12,AD=16,可求得CD,BC的长,又由EF⊥AB,∠ABC=60°,求得∠BFE=∠CFH=30°,然后由含30°的直角三角形的性质,求得BF,FC,CH,FH的长,然后由勾股定理求得DF的长.
解答 解:延长DC,EF相交于点H.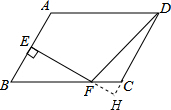
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD=12,AD=BC=16,
∵EF⊥AB,
∴∠B=∠FCH=60°,∠BEF=∠H=90°,
∴∠BFE=∠CFH=30°,
∵E是AB的中点,
∴BE=AE=$\frac{1}{2}$AB=6.
∴BF=2BE=12,
∴CF=BC-BF=4,
∴CH=$\frac{1}{2}$CF=2,
∴FH=$\sqrt{C{F}^{2}-C{H}^{2}}$=2$\sqrt{3}$,DH=CD+CH=14,
∴DF=$\sqrt{D{H}^{2}+F{H}^{2}}$=4$\sqrt{13}$.
故答案为:4$\sqrt{13}$.
点评 此题考查了平行四边形的性质、含30°角的直角三角形的性质以及勾股定理.注意准确作出辅助线是关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
12.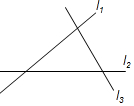 如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
 如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )| A. | 1处 | B. | 2处 | C. | 3处 | D. | 4处 |
 如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转7次,每次旋转45度形成的.
如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转7次,每次旋转45度形成的.