题目内容
研究下列算式，你会发现什么规律？
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52…
（1）请你找出规律并计算7×9+1 = 2
（2）用含有n的式子表示上面的规律：
（3）用找到的规律解决下面的问题：
计算：（1+
）（1+
）（1+
）（1+
）…（1+
）
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52…
（1）请你找出规律并计算7×9+1
（2）用含有n的式子表示上面的规律：
（3）用找到的规律解决下面的问题：
计算：（1+
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| 4×6 |
| 1 |
| 2011×2013 |
考点：规律型：数字的变化类
专题：
分析：（1）（2）观察发现一个正整数乘以比这个正整数大2的数再加1就等于这个正整数加1的平方，依此得到7×9+1=64=82；含有n的式子表示的规律．
（3）由（1+
）（1+
）=
×
×
×
=
得出（1+
）（1+
）（1+
）（1+
）…（1+
）=
知以上规律通分计算即可．
（3）由（1+
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| 4×6 |
| 1 |
| n(n+2) |
| 2n+1 |
| n+2 |
解答：解：（1）7×9+1=64=82；
（2）上述算式有规律，可以用n表示为：n（n+2）+1=（n+1）2；
（3）（1+
）（1+
）（1+
）（1+
）…（1+
）
=
=
．
（2）上述算式有规律，可以用n表示为：n（n+2）+1=（n+1）2；
（3）（1+
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| 4×6 |
| 1 |
| 2011×2013 |
=
| 2×(2011+1) |
| 2011+2 |
=
| 4024 |
| 2013 |
点评：此题考查数字的变化规律，找出数字之间的联系，得出规律解决问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
将△ABC的三个顶点的纵坐标不变，横坐标乘以-l后得到△DEF，则△DEF（ ）
| A、与△ABC关于x轴对称 |
| B、与△ABC关于y轴对称 |
| C、与△ABC关于原点对称 |
| D、向x轴的负方向平移了一个单位 |
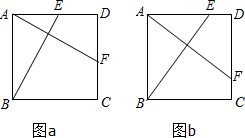如图ABCD是一个正方形花园．E、F是它的两个门且分别是AD、CD的中点，要修两条路BE和AF