题目内容
7.把关于x的方程x2+px+q=0化为(x+a)2=b形式,指出当p、q满足什么关系时,方程有实数根,并求出方程的根.分析 若一元二次方程有两不等实数根,则根的判别式△=b2-4ac>0,建立关于p、q的不等式,求出p、q的关系即可.
解答 解:x2+px+q=0,
x2+px=-q,
x2+px+($\frac{p}{2}$)2=-q+($\frac{p}{2}$)2
(x+$\frac{p}{2}$)2=$\frac{{p}^{2}-4q}{4}$,
∴当p2-4q≥0时,方程有实数根,
∴方程的根为x1=$\frac{-p+\sqrt{{p}^{2}-4q}}{2}$,x2=$\frac{-p-\sqrt{{p}^{2}-4q}}{2}$.
点评 本题考查了解一元二次方程-配方法,用配方法解一元二次方程的步骤:形如x2+px+q=0型:第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方即可.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
17.若a:b:c=3:4:12,则(2a+3b+4c):11a=( )
| A. | 1 | B. | 6 | C. | 4 | D. | 2 |
 已知:如图所示,AB=AC,CE=BD,点D、E分别在AB、AC上.
已知:如图所示,AB=AC,CE=BD,点D、E分别在AB、AC上.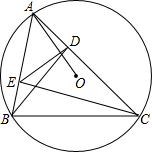 △ABC内接于⊙O,BD、CE为△ABC的两条高,试说明:AO⊥DE.
△ABC内接于⊙O,BD、CE为△ABC的两条高,试说明:AO⊥DE.