题目内容
11.求$\sqrt{a+4}$-$\sqrt{9-2a}$-$\sqrt{1-3a}$+$\sqrt{-{a}^{2}}$的值.分析 根据被开方数是非负数,可得不等式,根据解不等式组,可得a的值,根据实数的运算,可得答案.
解答 解:由$\sqrt{a+4}$-$\sqrt{9-2a}$-$\sqrt{1-3a}$+$\sqrt{-{a}^{2}}$有意义,得
$\left\{\begin{array}{l}{a+4≥0}\\{9-2a≥0}\\{1-3a≥0}\\{-{a}^{2}≥0}\end{array}\right.$,
解得a=0,
$\sqrt{a+4}$-$\sqrt{9-2a}$-$\sqrt{1-3a}$+$\sqrt{-{a}^{2}}$
=$\sqrt{4}$-$\sqrt{9}$-$\sqrt{1}$+$\sqrt{0}$
=2-3-1+0
=-2.
点评 本题考查了二次根式有意义的条件,利用被开方数是非负数得出不等式组是解题关键.

练习册系列答案
相关题目
6.已知关于x的方程ax2-2x+1=0,若a<0,那么方程的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
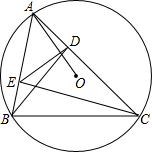 △ABC内接于⊙O,BD、CE为△ABC的两条高,试说明:AO⊥DE.
△ABC内接于⊙O,BD、CE为△ABC的两条高,试说明:AO⊥DE.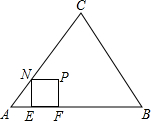 如图,正三角形ABC的边长为2$\sqrt{3}$.
如图,正三角形ABC的边长为2$\sqrt{3}$.