题目内容
若
+y2-4y+4=0,求xy的值.
| 2x+1 |
考点:配方法的应用,非负数的性质:偶次方,非负数的性质:算术平方根
专题:计算题
分析:已知等式变形,利用非负数的性质求出x与y的值,即可确定出xy的值.
解答:解:∵
+y2-4y+4=
+(y-2)2=0,
∴2x+1=0,y-2=0,
解得:x=-
,y=2,
则xy=-1.
| 2x+1 |
| 2x+1 |
∴2x+1=0,y-2=0,
解得:x=-
| 1 |
| 2 |
则xy=-1.
点评:此题考查了配方法的应用,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
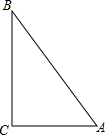 如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.