题目内容
12. 如图,O是△ABC内任意一点,试猜想:∠AOB与∠1、∠2、∠C之间的关系,并说明你猜想的正确性.
如图,O是△ABC内任意一点,试猜想:∠AOB与∠1、∠2、∠C之间的关系,并说明你猜想的正确性.
分析 延长CO交AB于E,再根据三角形的外角性质得出∠BOE=∠2+∠BCE,∠AOE=∠ACE+∠1,即可得出答案.
解答  解:∠AOB=∠1+∠2+∠C.
解:∠AOB=∠1+∠2+∠C.
延长CO交AB于E,
∵∠BOE是△BCO的外角,∠AOE是△ACO的外角,
∴∠BOE=∠2+∠BCE,∠AOE=∠ACE+∠1,
∴∠AOB=∠AOE+∠BOE=∠1+∠2+∠ACB,
即∠AOB=∠1+∠2+∠C.
点评 本题主要考查了三角形的外角性质的应用,作出辅助线,构造出三角形,再利用三角形内角与外角的关系求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各组数不能作为直角三角形的三边长的是( )
| A. | 1.5,2,3 | B. | 7,24,25 | C. | 9,12,15 | D. | 5,12,13 |
20. 如图,因为AB∥CD,可以( )
如图,因为AB∥CD,可以( )
 如图,因为AB∥CD,可以( )
如图,因为AB∥CD,可以( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠1=∠4 | D. | ∠1=∠5 |
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  平行四边形 | B. |  圆 | C. |  正五边形 | D. |  等腰三角形 |
 如图直角坐标系中,A(-2,1),B(-3,-2),平移线段AB,使B点的对应点刚好与坐标原点O重合.
如图直角坐标系中,A(-2,1),B(-3,-2),平移线段AB,使B点的对应点刚好与坐标原点O重合. 如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为(3,2$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标为(5,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为(3,2$\sqrt{3}$).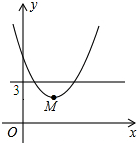 在平面直角坐标系中,点M是直线y=3与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{5}$x2+bx+c的顶点,则方程$\frac{1}{5}$x2+bx+c=2的解的个数是0,1或2.
在平面直角坐标系中,点M是直线y=3与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{5}$x2+bx+c的顶点,则方程$\frac{1}{5}$x2+bx+c=2的解的个数是0,1或2.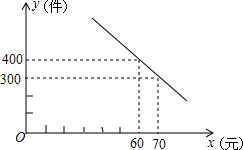 某服装厂销售一种成本为50元的衬衣,规定销售的单价不得低于成本价,又不能高于70元,销售量y(件)与销售单价x(元)的关系如图所示.
某服装厂销售一种成本为50元的衬衣,规定销售的单价不得低于成本价,又不能高于70元,销售量y(件)与销售单价x(元)的关系如图所示.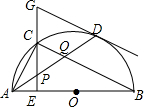 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是$\widehat{AD}$的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中正确结论是②③(只需填写序号).
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是$\widehat{AD}$的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中正确结论是②③(只需填写序号).