题目内容
把三角形的各边长度相应的缩小
，得到的三角形与原三角形相似，则其面积是原三角形面积的 ．
| 1 |
| 5 |
考点：相似三角形的性质
专题：
分析：利用相似三角形的性质，得出其相似比进而求出面积比．
解答：解：∵把三角形的各边长度相应的缩小
，
∴得到的三角形与原三角形相似比为：4：5，
∴其面积是原三角形面积的：(
)2=
．
故答案为：
．
| 1 |
| 5 |
∴得到的三角形与原三角形相似比为：4：5，
∴其面积是原三角形面积的：(
| 4 |
| 5 |
| 16 |
| 25 |
故答案为：
| 16 |
| 25 |
点评：此题主要考查了相似三角形的性质，得出两三角形的相似比是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
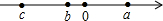有理数a，b，c在数轴上位置如图所示，则下列说法正确的是（ ）| A、a、b、c都表示正数 |
| B、b、c为正数，a为负数 |
| C、a、b、c都表示负数 |
| D、b、c为负数，a为正数 |
作出函数y=