题目内容
17.△ABC三个顶点为A(1,3),B(-1,-1),C(5,-4),则△ABC的形状是直角三角形.分析 首先根据两点间的距离公式求出AB,BC,AC的长度,然后根据勾股定理的逆定理即可确定该三角形为直角三角形.
解答 解:∵△ABC三个顶点为A(1,3),B(-1,-1),C(5,-4),
∴AB=$\sqrt{(1+1)^{2}+(3+1)^{2}}$=$\sqrt{20}$,BC=$\sqrt{(5+1)^{2}+(-4+1)^{2}}$=$\sqrt{45}$,AC=$\sqrt{(5-1)^{2}+(-4-3)^{2}}$=$\sqrt{65}$,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,
故答案为直角三角形.
点评 本题主要考查勾股定理的逆定理、两点间的距离公式,关键在于正确的计算出AB,BC,AC的长度,正确的运用相关的定理、公式.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
8.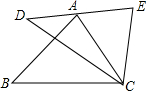 如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
 如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )| A. | AB=DE | B. | AB>DE | C. | AB<DE | D. | 不能确定 |
5.下列计算的结果正确的是( )
| A. | a+a=a2 | B. | a4-a2=a2 | C. | 3a+b=3ab | D. | a2-3a2=-2a2 |
6. 如图,点A、C、B在⊙O上,已知∠AOB=∠ACB=α.则α的值为( )
如图,点A、C、B在⊙O上,已知∠AOB=∠ACB=α.则α的值为( )
 如图,点A、C、B在⊙O上,已知∠AOB=∠ACB=α.则α的值为( )
如图,点A、C、B在⊙O上,已知∠AOB=∠ACB=α.则α的值为( )| A. | 135° | B. | 120° | C. | 110° | D. | 100° |
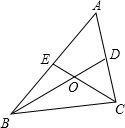 已知:如图,△ABC中,中线BD和中线CE相交于点O,求证:BO=2DO.
已知:如图,△ABC中,中线BD和中线CE相交于点O,求证:BO=2DO. 已知A(0,4)、B(6,2)表示两个村庄的位置,x轴表示公路的位置,请你在x轴上求一点P,使得AP+BP最小.
已知A(0,4)、B(6,2)表示两个村庄的位置,x轴表示公路的位置,请你在x轴上求一点P,使得AP+BP最小.