题目内容
19.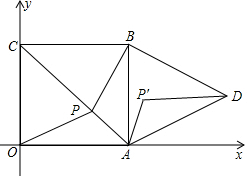 如图,正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,点P为对角线AC上的动点.
如图,正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,点P为对角线AC上的动点.(1)点B的坐标为(1,1),点D的坐标为(1+$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);当点P的坐标为($\frac{1}{2}$,$\frac{1}{2}$)时,PO+PB的值最小(坐标可保留根号);
(2)将AP绕点A顺时针旋转60度至AP′位置
①证明:BP=DP′;
②在线段AC上是否存在点P,使得BP+OP+AP的值最小?若不存在请说明理由;若存在,请简要说明理由并求出这个最小值(结果精确到0.1)
分析 (1)根据正方形和等边三角形的性质进行解答即可;
(2)①根据SAS证明△ABP与△ADP'全等,进而证明即可;
②当点P为对角线交点时BP+OP+AP的值最小,进而利用勾股定理解答即可.
解答 解:(1)∵正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,
∴点B的坐标为(1,1),点D的坐标为(1+$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
当点P为对角线交点时,即点P的坐标为($\frac{1}{2}$,$\frac{1}{2}$)时PO+PB的值最小;
故答案为:(1,1);(1+$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$);($\frac{1}{2}$,$\frac{1}{2}$);
(2)①∵正方形ABCO的边长为1,顶点A、C分别在x、y轴上,以AB为边向右作等边三角形ADB,
∴AB=AD,
∵将AP绕点A顺时针旋转60度至AP′位置,
∴∠PAB=∠P'AD,
∵在△ABP与△ADP'中,
$\left\{\begin{array}{l}{AP=AP'}\\{∠PAB=∠P'AD}\\{AB=AD}\end{array}\right.$,
∴△ABP≌△ADP'(SAS),
∴BP=DP′;
②当点P为对角线交点时BP+OP+AP的值最小,
∵BP+OP=OB=2PA=$\sqrt{2}$OA=$\sqrt{2}$,
∴BP+OP+AP=$\sqrt{2}+\frac{\sqrt{2}}{2}=\frac{3\sqrt{2}}{2}≈2$
点评 此题考查四边形综合题,关键是根据坐标与图形的特点进行分析,由正方形和等边三角形的性质解答.

练习册系列答案
相关题目
19.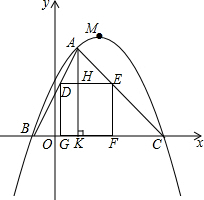 如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
(1)求出这条抛物线的解析式;
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
 如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:| x | … | -2 | 0 | 4 | 8 | 10 | … |
| y | … | 0 | 5 | 9 | 5 | 0 | … |
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
7. 如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
 如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )| A. | 4cm | B. | 5cm | C. | $\frac{15}{4}$cm | D. | $\frac{25}{4}$cm |
4.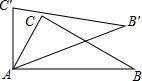 如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )
如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )
 如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )
如图所示,在△ABC中,∠CAB=70°,将△ABC绕点A旋转到△A′B′C′的位置,使得C′A⊥AB,则∠BAB′=( )| A. | 10° | B. | 20° | C. | 30° | D. | 50° |
9.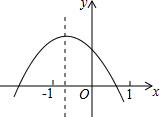 已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
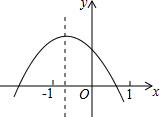 已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )| A. | a+b+c>0 | B. | b2-4ac<0 | C. | a-b+c>0 | D. | ab<0,c<0 |
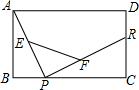 如图,已知矩形ABCD中,R是边CD的中点,P是边BC上一动点,E、F分别是AP、RP的中点,设BP的长为x,EF的长为y,当P在BC上从B向C移动时,y与x的大致图象是( )
如图,已知矩形ABCD中,R是边CD的中点,P是边BC上一动点,E、F分别是AP、RP的中点,设BP的长为x,EF的长为y,当P在BC上从B向C移动时,y与x的大致图象是( )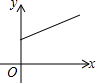
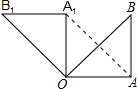 如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.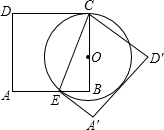 如图,矩形ABCD中,AD=4,O是BC边上的点,以OC为半径作⊙O交AB于点E,BE=$\frac{3}{5}$AE,把四边形AECD沿着CE所在的直线对折(线段AD对应A′D′),当⊙O与A′D′相切时,线段AB的长是$\frac{32}{9}$.
如图,矩形ABCD中,AD=4,O是BC边上的点,以OC为半径作⊙O交AB于点E,BE=$\frac{3}{5}$AE,把四边形AECD沿着CE所在的直线对折(线段AD对应A′D′),当⊙O与A′D′相切时,线段AB的长是$\frac{32}{9}$.