题目内容
13.某商场计划用5400元购买一批商品,若将进价降低10%,则可以多购买该商品30件.市场调查反映:售价为每件25元时,每天可卖出250件.如果调整价格,一件商品每涨价1元,每天要少卖出10件.(1)求该商品原来的进价;
(2)在进价没有改变的条件下,若每天所得的销售利润2000元时,且销量尽可能大,商品的售价是多少元;
(3)在进价没有改变的条件下,商场的营销部在调控价格方面,提出了A,B两种营销方案.
方案A:每件商品涨价不超过5元;方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
分析 (1)利用销量×每件利润=总利润,进而求出即可;
(2)利用二次函数的性质得出销售单价;
(3)分别求出两种方案的最值进而比较得出答案.
解答 解:(1)设该商品原来的进价为x元.
由题意:$\frac{5400}{x}$+30=$\frac{5400}{0.9x}$,解得x=20,
答:该商品原来的进价为20元.
(2)设提价x元,
根据题意得:(25+x-20)(250-10x)=2000,
解得x=15或5,
∵销量尽可能大,
∴x=5,
∴商品的售价是每件30元.
(3)w=(25+x-20)(250-10x)=-10x2+200x+1250=-10(x-10)2+2250(0≤x≤25);
∵-10<0,
抛物线对称轴是直线x=10,开口向下,对称轴左侧w随x的增大而增大,对称轴右侧w随x的增大而减小,
方案A:根据题意得,x≤5,则0≤x≤5,
当x=5时,利润最大,
最大利润为w=-10×52+200×5+1250=2000(元),
方案B:根据题意得,25+x-20≥16,
解得:x≥11,
则11≤x≤25,
故当x=11时,利润最大,
最大利润为w=-10×112+200×11+1250=2240(元),
∵2240>2000,
∴综上所述,方案B最大利润更高.
点评 此题主要考查了二次函数的应用,根据题意利用函数性质得出最值是解题关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
4.要调查姜堰城区八年级5000名学生了解“溱潼会船节”的情况,下列调查方式最合适的是( )
| A. | 在某校八年级选取100名女生 | |
| B. | 在某校八年级选取100名男生 | |
| C. | 在某校八年级选取100名学生 | |
| D. | 在城区5000名八年级学生中随机选取100名学生 |
3.以下数的绝对值是它本身的是( )
| A. | 0 | B. | 1,0 | C. | 1,-1 | D. | 1,-1或0 |
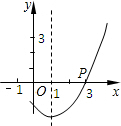 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论: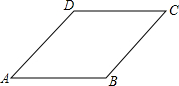 如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,那么点C、C1的距离为2$\sqrt{2}$.
如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,那么点C、C1的距离为2$\sqrt{2}$.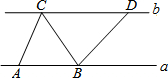 如图,直线a∥b,点A、B位于直线a上,点C、D位于直线b上,且AB:CD=2:3,如果△ABC的面积为6,那么△BCD的面积为9.
如图,直线a∥b,点A、B位于直线a上,点C、D位于直线b上,且AB:CD=2:3,如果△ABC的面积为6,那么△BCD的面积为9.