题目内容
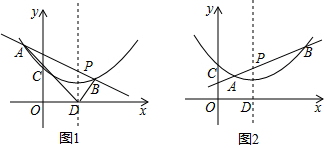
1.在菱形ABCD中,AB=2$\sqrt{3}$,AC是对角线,∠B=60°,点E在BC边上,点F在DC边上,且∠EAF=60°,AE与DC的延长线交于点M,AF与BC的延长线交于点N.(1)如图1,若点E为BC边上的中点.
①求证:△ACM≌△ACN;
②CM•NC的值是12.
(2)如图2,若点E为BC边上的任意点(不与点B,C重合),请说明CM•NC是一个定值.
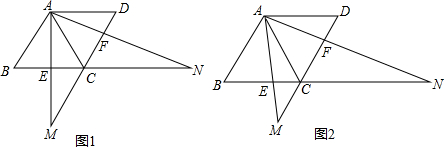
分析 (1)①由全等三角形的判定定理ASA证得结论;
②根据等腰三角形的判定得到CM=CA=2$\sqrt{3}$,结合①中全等三角形的性质得到CM=CN;
(2)由相似三角形△ACM∽△NCA的对应边成比例得到CM•NC=AC2=(2$\sqrt{3}$)2=12,即CM•NC是一个定值.
解答 (1)①证明,∵AC是菱形ABCD的对角线,∠B=60°,点E为BC边上的中点,
∴∠MAC=∠NAC=30°,∠ACD=∠ACB=60°,
∴∠ACM=∠ACN=120°.
在△ACM与△ACN中,
$\left\{\begin{array}{l}{∠MAC=∠NAC}\\{AC=AC}\\{∠ACM=∠ACN}\end{array}\right.$,
∴△ACM≌△ACN(ASA);
②解:∵∠MAC=30°,∠ACM=120°,
∴∠AMC=30°,
∴CM=CA=2$\sqrt{3}$,
∵△ACM≌△ACN,
∴CM=CN,
∴CM•NC=CM2=12.
故答案是:12;
(2)证明:∵∠EAF=60°,即∠MAC+∠NAC=60°.
又∠ACD=60°,
∴∠MAC+∠AMC=60°,
∴∠AMC=∠NAC.
又∠ACM=∠ACN=120°,
∴△ACM∽△NCA,
∴$\frac{AC}{NC}$=$\frac{CM}{CA}$,
由题意可知,△ABC是等边三角形,
∴AC=AB=2$\sqrt{3}$,
∴CM•NC=AC2=(2$\sqrt{3}$)2=12,即CM•NC是一个定值.
点评 本题综合考查了全等三角形的判定和性质,菱形的性质,相似三角形的判定和性质,等边三角形的判定和性质,熟练掌握菱形的性质是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
11.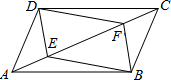 如图,点E,F是□ABCD对角线上两点,在条件①DE=BF;②∠ADE=∠CBF;③AF=CE; ④∠AEB=∠CFD中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( )
如图,点E,F是□ABCD对角线上两点,在条件①DE=BF;②∠ADE=∠CBF;③AF=CE; ④∠AEB=∠CFD中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( )
 如图,点E,F是□ABCD对角线上两点,在条件①DE=BF;②∠ADE=∠CBF;③AF=CE; ④∠AEB=∠CFD中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( )
如图,点E,F是□ABCD对角线上两点,在条件①DE=BF;②∠ADE=∠CBF;③AF=CE; ④∠AEB=∠CFD中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
9.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.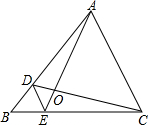 如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若AD=3BD,则S△DOE:S△AOC的值为( )
如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若AD=3BD,则S△DOE:S△AOC的值为( )
 如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若AD=3BD,则S△DOE:S△AOC的值为( )
如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若AD=3BD,则S△DOE:S△AOC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{16}$ |
6.下列事件为必然事件的是( )
| A. | 五边形的外角和是360° | B. | 打开电视机,它正在播广告 | ||
| C. | 明天太阳从西方升起 | D. | 抛掷一枚硬币,一定正面朝上 |
13.下列计算,正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | |$\frac{1}{2}$-2|=-$\frac{3}{2}$ | C. | $\root{3}{8}$=2$\sqrt{2}$ | D. | ($\frac{1}{2}$)-1=2 |
10.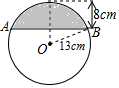 如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
 如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
如图,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )| A. | 10cm | B. | 16cm | C. | 24cm | D. | 26cm |