题目内容
16.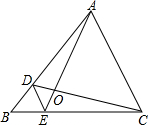 如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若AD=3BD,则S△DOE:S△AOC的值为( )
如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若AD=3BD,则S△DOE:S△AOC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{16}$ |
分析 根据AD=3BD,得出BD:AB=1:4;证明△DOE∽△AOC,得到$\frac{DE}{AC}$=$\frac{1}{4}$,由相似三角形的性质即可解决问题.
解答 解:∵AD=3BD,
∴BD:AB=1:4,
∵DE∥AC,
∴△BDE∽△BAC,
∴$\frac{DE}{AC}=\frac{BD}{AB}$
∴$\frac{DE}{AC}$=$\frac{1}{4}$,
∵DE∥AC,
∴△DOE∽△AOC,
∴S△DOE:S△AOC=($\frac{DE}{AC}$)2=$\frac{1}{16}$;
故选D.
点评 本题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用形似三角形的判定及其性质来分析、判断、推理或解答.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
6.如图是一个几何体的三视图,这个几何体是( )


| A. | 四棱柱 | B. | 三棱柱 | C. | 三棱锥 | D. | 圆锥 |
4.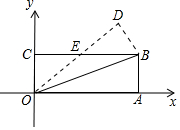 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )| A. | $y=\frac{4}{5}x$ | B. | $y=\frac{5}{4}x$ | C. | $y=\frac{3}{4}x$ | D. | $y=\frac{4}{3}x$ |
6.下列运算正确的是( )
| A. | (a2)m=a2m | B. | (2a)3=2a3 | C. | a3•a-5=a-15 | D. | a3÷a-5=a-2 |
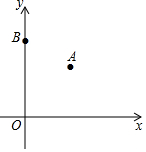 如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )
如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )
 如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.