题目内容
1.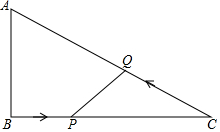 如图所示,在Rt△ABC中,∠B=90°,AB=3,BC=4,点P,Q分别从B,C两点同时出发匀速运动,其中点P以每秒1个单位的速度沿BC方向向点C运动,点Q以每秒2个单位的速度沿CA、AB方向运动,当点P到达C点时,点Q停止运动,假设运动时间为t秒.
如图所示,在Rt△ABC中,∠B=90°,AB=3,BC=4,点P,Q分别从B,C两点同时出发匀速运动,其中点P以每秒1个单位的速度沿BC方向向点C运动,点Q以每秒2个单位的速度沿CA、AB方向运动,当点P到达C点时,点Q停止运动,假设运动时间为t秒.(1)用含t的代数式表示线段PC、CQ的长,PC=4-t_,CQ=_2t或$\sqrt{{4}^{2}+(8-2t)^{2}}$;
(2)定义:到三角形两个顶点距离相等的点称为三角形的准外心.
①若点P为△ABC的准外心,试求CP的长;
②是否存在点P,使点P是△PCQ的准外心?若存在,求出PQ的长;若不存在,请说明理由.
分析 (1)PC=4-t,CQ分两种情形求解即可;
(2)①当P是BC中点时,点P是△ABC的准外心,此时PC=2.当PA=PB时,设PA=PC=x,在Rt△ABP中,根据PA2=AB2+PB2,列出方程即可解决问题;
②如图当P是△PQC的准外心,只有PQ=PC,此时点Q在线段AC上,作PE⊥AC于E.根据cos∠C=$\frac{EC}{PC}$=$\frac{BC}{AC}$=$\frac{4}{5}$,列出方程即可解决问题;
解答 解:(1)PC=4-t,
当0<t≤2.5时,CQ=2t,
当t>2.5时,CQ=$\sqrt{{4}^{2}+(8-2t)^{2}}$.
故答案为4-t,2t或$\sqrt{{4}^{2}+(8-2t)^{2}}$.
(2)①当P是BC中点时,点P是△ABC的准外心,此时t=2.
当PA=PB时,设PA=PC=x,
在Rt△ABP中,∵PA2=AB2+PB2,
∴x2=32+(4-x)2.
∴x=$\frac{25}{8}$,
综上所述,CP=2或CP=$\frac{25}{8}$
②如图当P是△PQC的准外心,只有PQ=PC,此时点Q在线段AC上,作PE⊥AC于E.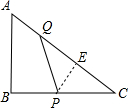
∵cos∠C=$\frac{EC}{PC}$=$\frac{BC}{AC}$=$\frac{4}{5}$,
∴$\frac{t}{4-t}$=$\frac{4}{5}$,
∴t=$\frac{16}{9}$,
∴PQ=PC=BC-PB=4-$\frac{16}{9}$=$\frac{20}{9}$.
点评 本题考查三角形综合题、勾股定理、准外心的定义,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
16.一元二次方程2x2-3x+5=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
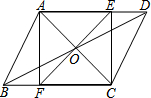 如图,在?ABCD中,对角线AC、BD相交于点O,直线EF经过点O,交AD于E,交BC于F,且AF⊥BC
如图,在?ABCD中,对角线AC、BD相交于点O,直线EF经过点O,交AD于E,交BC于F,且AF⊥BC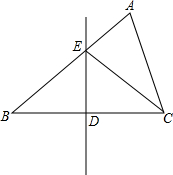 如图,在△ABC中,∠A=60°,边BC的垂直平分线分别交AB,BC于点E,D,连接EC.若∠B=∠ACE,求∠B的度数.
如图,在△ABC中,∠A=60°,边BC的垂直平分线分别交AB,BC于点E,D,连接EC.若∠B=∠ACE,求∠B的度数.