题目内容
19.给出下列几组数:①6,7,8;②8,15,6;③n2-1,2n,n2+1;④$\sqrt{2}$+1,$\sqrt{2}$-1,$\sqrt{6}$.其中能组成直角三角形的三条边长是( )| A. | ①③ | B. | ②④ | C. | ①② | D. | ③④ |
分析 判定是否为直角三角形,这里给出三边的长,只要验证两小边的平方和是否等于最长边的平方即可.
解答 解:①62+72≠82,故不是直角三角形,故错误;
②62+82≠152,故不是直角三角形,故错误;
③(n2-1)2+(2n)2=(n2+1)2,故是直角三角形,故正确;
④($\sqrt{2}$-1)2+($\sqrt{2}$+1)2=62,故是直角三角形,故正确.
正确的是③④.
故选:D.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.在△ABC中,已知∠A=∠B=45°,BC=$\sqrt{2}$,则边AB的长为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
10.统计得到一组数据,其中最大值是136,最小值是52,取组距为10,可以分成( )
| A. | 10组 | B. | 9组 | C. | 8组 | D. | 7组 |
14.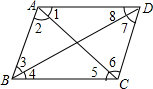 如图,如果AD∥BC,则下列结论正确的是( )
如图,如果AD∥BC,则下列结论正确的是( )
 如图,如果AD∥BC,则下列结论正确的是( )
如图,如果AD∥BC,则下列结论正确的是( )| A. | ∠1=∠4 | B. | ∠2=∠6 | C. | ∠3=∠7 | D. | ∠4=∠8 |
11.下列调查方式,你认为最合适的是( )
| A. | 了解恒安新区每天的流动人口数,采用抽样调查方式 | |
| B. | 要了解全市七年级学生英语单词的掌握情况,采用全面调查方式 | |
| C. | 了解矿区居民日平均用水量,采用全面调查方式 | |
| D. | 旅客进火车站上车前的安检,采用抽样调查方式 |
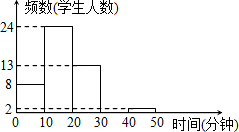 李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50min,然后将调查数据整理,作出如图15所示的频数直方图的一部分.
李老师为了了解本班学生作息时间,调查班上50名学生上学路上所花的时间,他发现学生所花时间都少于50min,然后将调查数据整理,作出如图15所示的频数直方图的一部分.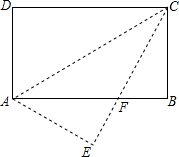 如图,在矩形ABCD中,AB=16,BC=8,将矩形沿AC折叠,点D落在点E处,CE与AB交于点F.
如图,在矩形ABCD中,AB=16,BC=8,将矩形沿AC折叠,点D落在点E处,CE与AB交于点F.