题目内容

20．一种复读机原价为100元，经过两次降价后，现价为64元，若每次降价的百分率相同，设这个百分率为x，则下列方程正确的是（　　）
A．100（1+x）2=64B．100（1-x）2=64C．100（1-x2）=64D．100（1+x2）=64

分析 增长率问题，一般用增长后的量=增长前的量×（1+增长率），本题可参照增长率问题求解．如果每次降价的百分率相同，设为x，根据题意可用x分别表示两次降价后的价格，然后根据题意即可列出方程．

解答 解：设每次降价的百分率为x，
依题意得100（1-x）2=64．
故选：B．

点评 本题考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b（当增长时中间的“±”号选“+”，当降低时中间的“±”号选“-”）．

练习册系列答案
相关题目
10．函数y=$\frac{1}{{x}^{2}-2x-3}$中，自变量的取值范围是x≠3且x≠-1．
11．下列计算正确的是（　　）
A．3$\sqrt{2}$-$\sqrt{2}$=3B．$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$C．（2$\sqrt{5}$）2=10D．$\sqrt{（-3）^{2}}=-3$
8．某果园2011年水果产量为100吨，2013年水果产量为144吨，求这两年该果园水果产量的年平均增长率．
15．计算：$\sqrt{12}+{（-1）^{2015}}-{（π-\sqrt{3}）^0}+{（\frac{1}{2}）^{-2}}-|{-3}|+\root{3}{8}$．
5．为了美化城市，建设中的某休闲广场准备用边长相同的正三角形与正方形两种地转镶嵌地面，在每一个顶点的周围，正三角形、正方形地转的个数分别是（　　）
A．3，2B．2，3C．4，1D．2、2
12．为庆祝元旦，市政部门准备用灯饰美化紫薇路．需采用A、B两种不同类型的灯笼500个，且B灯笼的个数是A灯笼个数的$\frac{2}{3}$．
（1）求A、B两种灯笼各需多少个？
（2）已知A、B两种灯笼的单价分别为50元、60元，则这次美化工程购置灯笼需多少费用？
9．计算：
（1）-6$\frac{2}{5}$+21-1.5-（-4$\frac{2}{5}$）+（-9）-（-1.5）
（2）-（$\frac{1}{2}$）2÷$\frac{1}{8}$-（$\frac{1}{3}$-$\frac{1}{4}$）×（-12）
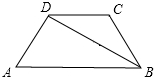10．如图，在四边形ABCD中，DC∥AB，对角线BD平分∠ABC，且BD⊥AD，若AD=2，CD=3，则对角线BD的长为4$\sqrt{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网