题目内容
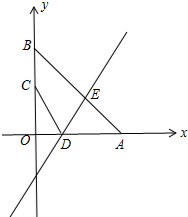如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在x轴、y轴上，且OA、OB的长满足方程x2-16x+64=0．（1）求点A、B的坐标；
（2）将点A翻折落在线段OB的中点C处，折痕交OA于点D，交斜边于点E，求直线DE的解析式；
（3）在（2）的条件下，在平面直角坐标系内，是否存在点F使点A、D、E、F为顶点的四边形是平行四边形？若存在请直接写出点F的坐标；若不存在，请说明理由．
考点：一次函数综合题
专题：
分析：（1）解方程可求得OA=OB=8，可求得A、B坐标；
（2）设DE交y轴于点M，利用勾股定理分别求得D、M的坐标，可求得DE的解析式；
（3）可先求得E点的坐标，分F点在x轴上方和下方分别讨论，在x轴上方时利用平行线的交点可求得F点的坐标，在x轴下方时可求对角线和过A点平行于x轴的直线的交点可求得F的坐标．
（2）设DE交y轴于点M，利用勾股定理分别求得D、M的坐标，可求得DE的解析式；
（3）可先求得E点的坐标，分F点在x轴上方和下方分别讨论，在x轴上方时利用平行线的交点可求得F点的坐标，在x轴下方时可求对角线和过A点平行于x轴的直线的交点可求得F的坐标．
解答：解：（1）解方程x2-16x+64=0可知方程的两根为x=8，
∴OA=OB=8，
∴A为（8，0），B为（0，8）；
（2）∵点A翻折落在线段OB的中点C处，
∴DE垂直平分AC，
∴DA=DC，
设OD为x，则DA=DC=OA-AD=8-x，
又∵C为OB中点，
∴OC=4，
在Rt△OCD中，由勾股定理可得（8-x）2=42+x2，解得x=3，
∴D为（3，0），
设DE与y轴交于点M，设M为（0，y），连接MA，如图1，
则OM=-y，且MA=MC=4-y，
在Rt△OAM中，由勾股定理可得（4-y）2=y2+82，解得y=-6，
∴M为（0，-6），
设直线DE为y=kx+b，
把D、M坐标代入可求得k=2，b=-6，
∴直线DE解析式为y=2x-6；
（3）设直线AB解析式为y=mx+n，
把A、B坐标代入可求得m=-1，n=8，
∴直线AB的解析式为y=-x+8，
联立直线AB和直线DE解析式可得
，解得
，
∴E点为（
，
），
当F在x轴上方时，
过E点作EF∥x轴，则直线EF方程为y=
，
①当AF∥DE时，过A作AF∥DE，交EF于点F，如图2，
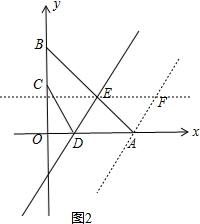
∵直线DE解析式为y=2x-6，
∴设直线AF解析式为y=2x+s，且过A点，
把A点坐标代入可求得s=-16，
∴直线AF的解析式为y=2x-16，
联立直线AF和直线EF解析式可求得F点坐标为（
，
），
②当DF∥AE时，过D作DF∥AE，交EF于点F，如图3，
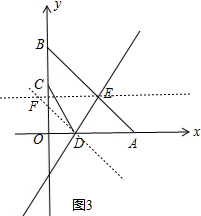
∵直线AB的解析式为y=-x+8，
∴设直线DF解析式为y=-x+r，且过D点，
把D点坐标代入可求得r=3，
∴直线DF的解析式为y=-x+3，
联立直线DF和EF解析可求得F点坐标为（-
，
），
当F在x轴下方时，如图4，则有AE∥DF，DE∥AF，
可求得直线AF的解析式为y=2x-16，直线DF解析式为y=-x+3，
联立可求得F点的坐标为（
，-
），
综上可知存在点F使点A、D、E、F为顶点的四边形是平行四边形，其坐标为（
，
）或（-
，
）或（
，-
）．
∴OA=OB=8，
∴A为（8，0），B为（0，8）；
（2）∵点A翻折落在线段OB的中点C处，
∴DE垂直平分AC，
∴DA=DC，
设OD为x，则DA=DC=OA-AD=8-x，
又∵C为OB中点，
∴OC=4，
在Rt△OCD中，由勾股定理可得（8-x）2=42+x2，解得x=3，
∴D为（3，0），
设DE与y轴交于点M，设M为（0，y），连接MA，如图1，
则OM=-y，且MA=MC=4-y，
在Rt△OAM中，由勾股定理可得（4-y）2=y2+82，解得y=-6，
∴M为（0，-6），
设直线DE为y=kx+b，
把D、M坐标代入可求得k=2，b=-6，
∴直线DE解析式为y=2x-6；
（3）设直线AB解析式为y=mx+n，
把A、B坐标代入可求得m=-1，n=8，
∴直线AB的解析式为y=-x+8，
联立直线AB和直线DE解析式可得
|
|
∴E点为（
| 14 |
| 3 |
| 10 |
| 3 |
当F在x轴上方时，
过E点作EF∥x轴，则直线EF方程为y=
| 10 |
| 3 |
①当AF∥DE时，过A作AF∥DE，交EF于点F，如图2，
∵直线DE解析式为y=2x-6，
∴设直线AF解析式为y=2x+s，且过A点，
把A点坐标代入可求得s=-16，
∴直线AF的解析式为y=2x-16，
联立直线AF和直线EF解析式可求得F点坐标为（
| 29 |
| 3 |
| 10 |
| 3 |
②当DF∥AE时，过D作DF∥AE，交EF于点F，如图3，
∵直线AB的解析式为y=-x+8，
∴设直线DF解析式为y=-x+r，且过D点，
把D点坐标代入可求得r=3，
∴直线DF的解析式为y=-x+3，
联立直线DF和EF解析可求得F点坐标为（-
| 1 |
| 3 |
| 10 |
| 3 |
当F在x轴下方时，如图4，则有AE∥DF，DE∥AF，
可求得直线AF的解析式为y=2x-16，直线DF解析式为y=-x+3，
联立可求得F点的坐标为（
| 19 |
| 3 |
| 10 |
| 3 |
综上可知存在点F使点A、D、E、F为顶点的四边形是平行四边形，其坐标为（
| 29 |
| 3 |
| 10 |
| 3 |
| 1 |
| 3 |
| 10 |
| 3 |
| 19 |
| 3 |
| 10 |
| 3 |
点评：本题主要考查待定系数法求函数解析式和轴对称的性质、平行四边形的性质及直线交点的求法等知识的综合应用．掌握好待定系数法就函数解析式是解题的关键，在（2）中注意线段垂直平分线上的点到线段两端点的距离相等，在（3）中确定出点F的位置是解题的关键，利用直线的交点求其坐标是常用的方法．注意方程思想的应用．
练习册系列答案
相关题目
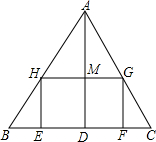如图，△ABC是一张锐角三角形的硬纸片，AD是边BC上的高，BC=40cm，AD=30cm．从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH，使它的一边EF在BC上，顶点G，H分别在AC，AB上，AD与HG的交点为M．