题目内容
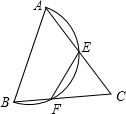
将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．已知AB=AC=3，BC=4，若以点B′、F、C为顶点的三角形与△ABC相似，那么BF的长度是______．
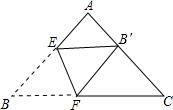
根据△B′FC与△ABC相似时的对应关系，有两种情况：
①△B′FC∽△ABC时，
=
，
又∵AB=AC=3，BC=4，B′F=BF，
∴
=
，
解得BF=
；
②△B′CF∽△BCA时，
=
，
AB=AC=3，BC=4，B′F=CF，BF=B′F，
而BF+FC=4，即2BF=4，
解得BF=2．
故BF的长度是
或2．
故答案为：
或2．
①△B′FC∽△ABC时，
| B′F |
| AB |
| CF |
| BC |
又∵AB=AC=3，BC=4，B′F=BF，
∴
| BF |
| 3 |
| 4-BF |
| 4 |
解得BF=
| 12 |
| 7 |
②△B′CF∽△BCA时，
| B′F |
| BA |
| CF |
| CA |
AB=AC=3，BC=4，B′F=CF，BF=B′F，
而BF+FC=4，即2BF=4，
解得BF=2．
故BF的长度是
| 12 |
| 7 |
故答案为：
| 12 |
| 7 |
练习册系列答案
相关题目
重合），过动点P作PD
